408490: GYM103150 D Moving Points

D. Moving Pointstime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

There are $$$n^2$$$ points on the coordinate plane, at the locations $$$$$$ \begin{matrix} (1,1), & (1,2), & \cdots & (1,n), \\ (2,1), & (2,2), & \cdots & (2,n), \\ \vdots & \vdots & \ddots & \vdots \\ (n,1), & (n,2), & \cdots & (n,n). \\ \end{matrix} $$$$$$ More formally, the initial set of points $$$S = \{(i,j) \mid 1 \leq i, j \leq n\}$$$.

You want to move each point to a different point such that

• the distance each point moves is at least $$$\sqrt{d}$$$, and
• the set of resulting points equals the set of initial points. That is, after all the points have moved, they occupy the same locations as before. (More formally, the final set of points equals $$$S$$$.)

Given $$$n$$$ and $$$d$$$, find any such movement or report that it does not exist.

Input

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 150$$$) — the number of test cases.

The only line of each test case contains two space-separated integers $$$n$$$ and $$$d$$$ ($$$2 \leq n \leq 300$$$, $$$1 \leq d \leq 10^9$$$) — the range of points and the square of the minimum distance each point must move, respectively.

The sum of $$$n$$$ over all test cases does not exceed $$$300$$$.

Output

For each test case, if such a movement is impossible, output NO.

Otherwise, output YES followed by $$$n^2$$$ lines. Each line should contain four space separated integers $$$x_i$$$, $$$y_i$$$, $$$x'_i$$$, $$$y'_i$$$ ($$$1 \leq x_i, y_i, x'_i, y'_i \leq n$$$), representing that the point $$$(x_i, y_i)$$$ moves to the point $$$(x'_i, y'_i)$$$. The resulting points should satisfy the conditions in the problem statement.

If there are multiple possible movements, print any of them.

ExampleInput

5
2 1
2 2
2 3
4 1
5 15

Output

YES
1 1 1 2
1 2 2 2
2 2 2 1
2 1 1 1
YES
1 1 2 2
1 2 2 1
2 1 1 2
2 2 1 1
NO
YES
1 1 1 2
1 2 1 1
1 3 1 4
1 4 1 3
2 1 2 2
2 2 2 1
2 3 2 4
2 4 2 3
3 1 3 2
3 2 3 1
3 3 3 4
3 4 3 3
4 1 4 2
4 2 4 1
4 3 4 4
4 4 4 3
NO

Note

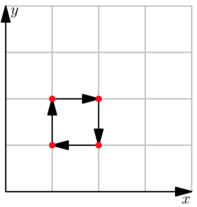
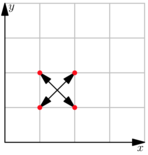
The picture below shows the movement for the first test case. Each point moves at least $$$\sqrt{1}$$$ units, and the set of resulting points is the set of initial points.

The picture below shows the movement for the second test case. Each point moves at least $$$\sqrt{2}$$$ units, and the set of resulting points is the set of initial points. It can be shown that no such movement exists for the third test case.