408352: GYM103104 C Data structure

C. Data structuretime limit per test2 secondsmemory limit per test512 megabytesinputstandard inputoutputstandard output

At 8 o'clock in the morning, Little W and Little N are taking a data structure class. The teacher is talking about Huffman trees and Huffman coding.

In case you are not familiar with Huffman trees, here is a formal definition for it: for a given sequence $$$(w_1,...,w_n)$$$, the Huffman tree generated by $$$(w_1,...,w_n)$$$ is defined as the rooted binary tree of $$$n$$$ leaves which minimizes the value of $$$\mathrm{WPL}=\sum_{i=1}^nw_id_i$$$, where $$$d_i$$$ denotes the depth of the $$$i$$$-th leaf of the tree. Recall that the leaves of a rooted tree are the non-root nodes that are connected to only one edge, and the depth of a node is defined as the number of edges of the simple path from the node to the root.

Little W is quite interesting in Fibonacci sequence recently, so he writes down the first $$$K$$$ numbers $$$F_1,F_2,...,F_K$$$ of the sequence. Recall that the Fibonacci sequence is a sequence satisfying $$$F_i=F_{i-1}+F_{i-2}$$$ for any $$$i\geq 3$$$, and in this problem $$$F_1=F_2=1$$$. He then draws an illustration of the Huffman tree generated by the $$$K$$$ numbers $$$(F_1,...,F_k)$$$. Note that for a sequence of numbers, there may be many kinds of valid Huffman trees, and he will choose the one with the lexicographically smallest middle order (only leaf node). Little W is bored, so he paints Huffman the tree with distinct colors on each node. Let's name the tree $$$\mathcal{W}$$$. The following picture contains two examples.

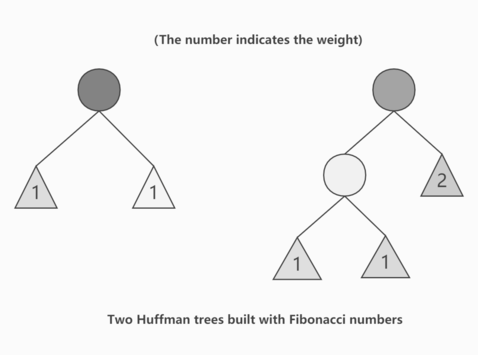
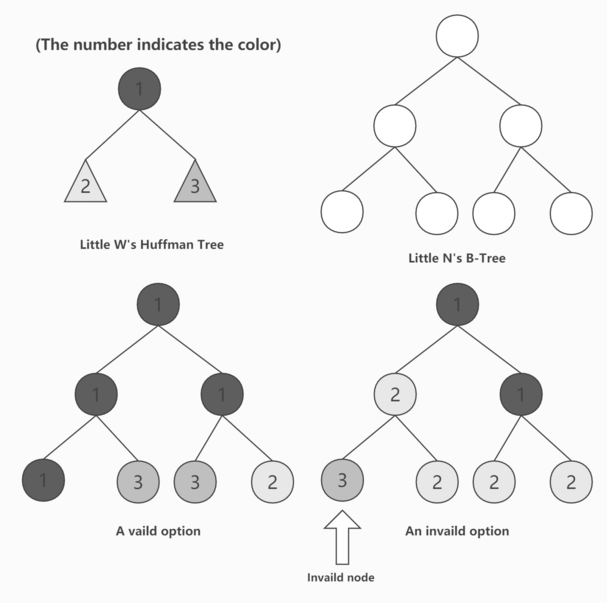
Little N has a crush on Little W recently and wants to attract his attention, so she wants to paint a tree similar to Little W's. She opens the textbook and finds a B-tree illustration and starts to paint it with color. This is a B-tree of $$$M$$$ order and $$$N$$$ nodes. You can simply consider a B-tree of $$$M$$$ order as a tree in which each internal node has at least $$$\lceil M/2 \rceil$$$ children and at most $$$M$$$ children (an internal node is a node that is neither a leaf nor the root), while the root node can have less than $$$\lceil M/2 \rceil$$$ children, and all leaf nodes have the same depth. Let's name the B-tree $$$\mathcal{N}$$$.

A painting option of $$$\mathcal{N}$$$ is considered to be similar to $$$\mathcal{W}$$$ if the following conditions are met:

• The colors used in $$$\mathcal{N}$$$ appear in $$$\mathcal{W}$$$.
• The root of $$$\mathcal{N}$$$ and the root of $$$\mathcal{W}$$$ shares the same color.
• For any non-root node $$$u$$$ in $$$\mathcal{N}$$$ with its father node $$$v$$$, if they don't share the same color, then the color of $$$u$$$ must be a son-color of the color of $$$v$$$ in $$$\mathcal{W}$$$. Formally, let's define the color of $$$u$$$ as $$$A$$$, the color of $$$v$$$ as $$$B$$$, and $$$\mathrm{Node_w}(X)$$$ as the node with color $$$X$$$ in $$$\mathcal{W}$$$. Then the following must be held: $$$A=B$$$, or $$$\mathrm{Node_w}(A)$$$ is the son of $$$\mathrm{Node_w}(B)$$$.

For example, in this picture below, the number indicates the color. The node which we figure out is invaild because color 3's father must be 3 or 1 (according to Little W's Huffman tree).

Can you help Little N find out how many painting options similar to $$$\mathcal{W}$$$ there are? As the answer may be huge, you just need to print it modulo 998244353.Input

The first line contains a single integer $$$T$$$ ($$$1 \le T \le 10$$$) — the number of test cases.

The first line of each test case contains three integers $$$K$$$ ($$$1\le K \le 1000000$$$) , $$$M$$$ ($$$3\le M \le 10$$$) and $$$N$$$ ($$$1\le N \le 1000000$$$) , indicating the length of Fibonacci sequence, the order of B-tree and the number of nodes in B-tree. Attention that we won't give you Little W's Huffman tree directly, and you need to build it yourself.

The second line of each test case contains $$$N-1$$$ integers, the $$$i$$$-th integer $$$x_i$$$($$$1\le x_i \le N$$$) indicating that in Little N's B-tree the father of node $$$i+1$$$ is $$$x_i$$$, it's guaranteed that node $$$1$$$ is the root.

It's guaranteed that the sum of $$$N$$$ over test cases doesn't exceed $$$1000000$$$ and the sum of $$$K$$$ doesn't exceed $$$1000000$$$.

Output

For each test case, one integer in a single line indicating the answer (modulo 998244353).

ExampleInput

2
2 3 3
1 1
3 3 7
1 1 2 2 3 3

Output

9
361