408202: GYM103053 A Sorted Pairwise Distance List

Korone just bought $$$2 \leq N \leq 3,000$$$ Yubi's, which is one of her favorite snacks. The snacks are labelled $$$0,1,...N-1$$$. To stop herself from eating it all at once, she decided to bury the snacks in her backyard. She will bury each snack at some non-negative integer coordinates $$$(X, Y)$$$ where $$$0 \leq X \leq 100,000$$$ and $$$0 \leq Y \leq 100,000$$$. Multiple Yubi's can be buried at the same coordinate.

After burying the snacks, she thought that it is only obvious to consider the Sorted Pairwise Distance List (SPDL), which is just the list of all distances between any distinct unordered pair of snacks, sorted in non-decreasing order. Here we define the distance between a pair of points $$$P=(X_P,Y_P)$$$ and $$$Q=(X_Q,Y_Q)$$$ as $$$(X_P-X_Q)^2 + (Y_P-Y_Q)^2$$$. Unless stated otherwise, any mention of distance will be referring to this definition.

She will perform $$$1 \leq Q \leq 3,000$$$ changes. In each change, she will dig up one of the snack, and rebury it somewhere else, again at integer coordinates $$$X_{new}, Y_{new} \leq 100,000$$$. She wants to know that after each change, does the SPDL become lexicographically larger, smaller, or remain equal? See notes for a formal definition of lexicographical order.

In the first sample, suppose that she bought $$$N = 4$$$ Yubi's, buried at $$$P_0=(0,0)$$$, $$$P_1=(4,0)$$$, $$$P_2=(0,3)$$$, $$$P_3=(5,5)$$$, then the SPDL is $$$L_0 = \{9,16,25,26,29,50\}$$$, contributed by the distances of pair $$$\{(P_0,P_2),(P_0,P_1),(P_1,P_2),(P_1,P_3),(P_2,P_3),(P_0,P_3)\}$$$. The positions and their Euclidean distances (which is just the square root of our distance) are illustrated below.

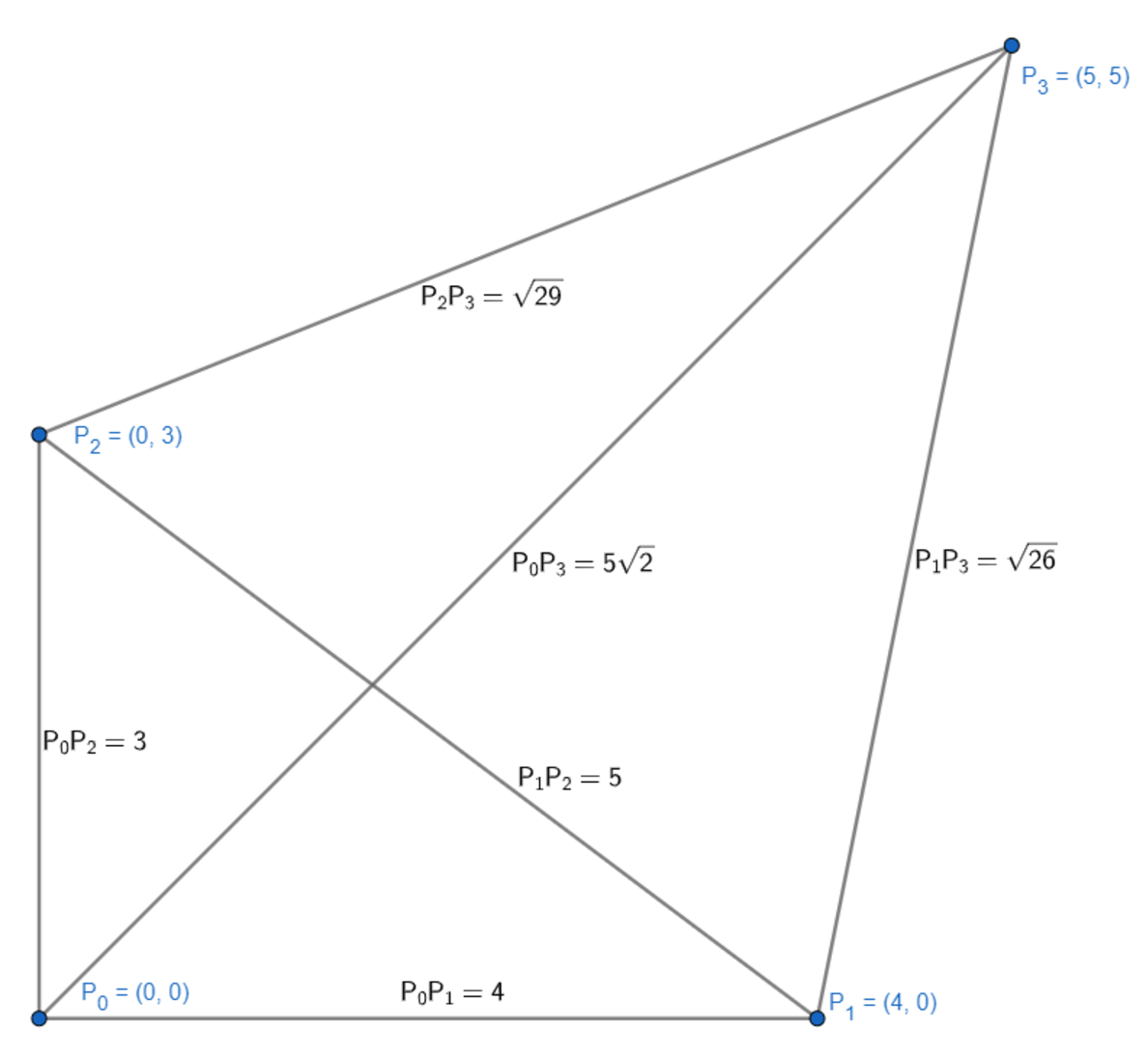
Suppose that she then digs up $$$P_3$$$ and reburies it at $$$(1,2)$$$. The SPDL then becomes $$$L_1 = \{2,5,9,13,16,25\}$$$ instead. The smallest index where $$$L_0 \neq L_1$$$ is $$$0$$$ and the $$$0^{th}$$$ element in $$$L_1$$$ is smaller than in $$$L_0$$$, hence the SPDL became smaller.

She told her trusted friend Risuna "Have confidence!" and tasked them with this job. But Risuna has no confidence of doing it correctly and seeks your help. Can you help Risuna out?

The first line consists of two integers, $$$N$$$ and $$$Q$$$, denoting the number of Yubi's and the number of changes.

Then $$$N$$$ lines follow. The $$$i^{th}$$$ line of the $$$N$$$ lines ($$$0$$$-indexed) contains two integers, representing the initial coordinate of the $$$i^{th}$$$ Yubi.

Then $$$Q$$$ lines follow. Each line is represented by the three integers $$$W, X_{new}, Y_{new}$$$ representing the change $$$W^{th}$$$ Yubi (also $$$0$$$-indexed) being reburied to location $$$(X_{new}, Y_{new})$$$

After each change, output one line "larger", "smaller", or "equal" (without quotes) denoting if the SPDL became lexicographically larger, smaller or remain equal respectively.

Subtask 1 (23 points): $$$N,Q \leq 300$$$, $$$X,Y,X_{new},Y_{new} \leq 3,000$$$

Subtask 2 (43 points): $$$X,Y,X_{new},Y_{new} \leq 100$$$

Subtask 3 (21 points): $$$X,Y,X_{new},Y_{new} \leq 3,000$$$

Subtask 4 (13 points): No additional constraints

4 1
0 0
4 0
0 3
5 5
3 1 2

smaller

4 3
1 1
0 2
5 3
0 5
1 5 5
1 4 1
2 5 3

larger
larger
equal

Consider two lists $$$A$$$ and $$$B$$$ of the same length. Let $$$A_i$$$ denote the $$$i^{th}$$$ element of $$$A$$$, similarly for $$$B$$$. If both $$$A$$$ and $$$B$$$ are the same ($$$A_i = B_i$$$ for all $$$i$$$), then we say they are lexicographically equal.

If not, let $$$k$$$ be the smallest index such that $$$A_k \neq B_k$$$. Then we say $$$A$$$ is lexicographically smaller than $$$B$$$ is $$$A_k < B_k$$$, otherwise $$$A$$$ is lexicographically larger.