408097: GYM102985 D Peter Piper Picked the Perfect Piece of Pizza

Peter Piper is attending a pizza party with his closest pals, and he is determined to pick the perfect, most optimal piece of pizza. Paris, who purchased the rectangular pizzas, is preparing to cut the most superb pie, topped with both pineapple and pepperoni. Peter pays close attention as she cuts the pan pizza in horizontal and vertical lines across, because he knows that once she is finished cutting, he will have mere moments to locate and snatch up the largest slice.

Help Peter pick out the perfect piece of pizza! Compute the location of the largest pizza slice!

The first line of input will contain four integers, $$$L$$$, $$$W$$$, $$$H$$$, and $$$V$$$. The first two integers $$$L$$$ and $$$W$$$ ($$$1 \leq L, W \leq 10^{9}$$$) represent the length and width of the pan pizza respectively. Then $$$H$$$ and $$$V$$$ denote the number of horizontal and the number of vertical cuts that Paris makes into the pizza respectively, where $$$(1 \leq H \leq min(L, 10^{3}))$$$ and $$$(1 \leq V \leq min(W, 10^{3}))$$$.

The next line of input contains $$$H$$$ integers $$$h_i$$$, where each $$$h_i$$$ ($$$0 < h_i < L$$$) represents the height coordinate of a horizontal cut. Then the third and last line of input contains $$$V$$$ integers $$$v_i$$$, where each $$$v_i$$$ ($$$0 < v_i < W$$$) represents the width coordinate of a vertical cut. Note that no two horizontal lines and no two vertical lines will ever overlap.

Find the biggest pizza slice! On one line, output two coordinate pairs specifying the upper-left corner and then the lower-right corner of the perfect piece in the pan. Print the coordinate pairs simply as space-separated integers, listing the vertical coordinate before the horizontal coordinate for each pair.

In the case of a tie between multiple equally-sized pizza slices, Peter will pick the slice closest to top of the pan (0 length) where he is standing, and if there is still a tie after that, then he will pick the slice closest to the left side of the pan (0 width).

15 25 4 7
2 7 4 12
15 19 3 6 8 2 14

8 7 14 12

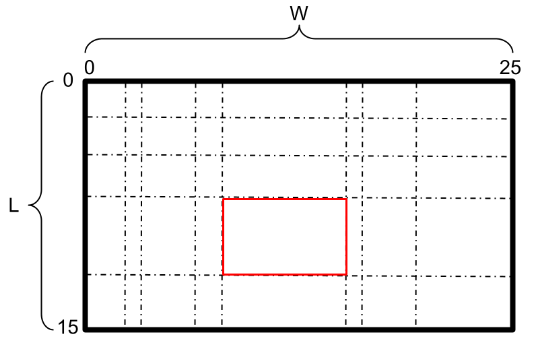
The diagram below provides a layout of the superb pizza in the sample case after Paris has finished cutting it. The largest slice she cuts turns out to be the piece defined by points ($$$8, 7$$$) and ($$$14, 12$$$) with an area of 30. Note that the piece defined by points ($$$19, 7$$$) and ($$$25, 12$$$) is tied for size but is located further to the right side of the pan than Peter's perfect piece.