408076: GYM102979 D Designing a PCB

Dongkyu is trying to design a single-sided printed circuit board (PCB for short). A PCB is composed of pads on which components can be mounted, and conductive tracks connecting the pads. You can think of a PCB as an infinite two-dimensional plane, a pad as a point on the plane, and a track as a connected polyline on the plane.

In the circuit that Dongkyu wants to design, the $$$2n$$$ pads are arranged horizontally. The $$$i$$$-th pad from the left is located at coordinate $$$(i - 1, 0)$$$. Each pad is assigned a label: an integer between $$$1$$$ and $$$n$$$, inclusive. For each $$$1 \le i \le n$$$, there are exactly 2 pads labeled with $$$i$$$.

Dongkyu needs to draw $$$n$$$ tracks to connect the pairs of pads with the same label. Each track must be a polyline consisting of segments of positive integer lengths, such that each segment is parallel to one of the coordinate axes. They start and end at the points representing the pads. No two tracks may share a common point.

Given the number of pads and the labeling, write a program to design the circuit.

The first line of input contains a single integer $$$n$$$ ($$$1 \le n \le 1000$$$).

The second line contains $$$2 n$$$ integers $$$p_i$$$ ($$$1 \le p_i \le n$$$). Here, $$$p_i$$$ is the label on the $$$i$$$-th pad from the left. It is guaranteed that each integer between $$$1$$$ and $$$n$$$ appears exactly twice in the labels.

If it is impossible to design a circuit conforming to the limitations described in the statement, print "NO".

Otherwise, print "YES" on the first line. Then, on the next $$$n$$$ lines, output the descriptions of $$$n$$$ tracks in order of increasing label number of the pads they are connecting.

Each track must be a polyline starting from the leftmost of the two connected pads. The description of a track starts with one integer $$$L_i$$$ ($$$1 \le L_i \le 10$$$) describing the number of segments forming the track. Each segment is described by one letter for the direction, followed by a positive integer for the segment length. The directions are: 'D' — down (decreasing $$$y$$$), 'U' — up (increasing $$$y$$$), 'R' — right (increasing $$$x$$$), and 'L' — left (decreasing $$$x$$$). The segments must be listed from the starting pad to the ending pad in the order they are connected.

Each polyline must have no self-intersections and no self-touchings. Different polylines must have no common points. The resulting coordinates of the vertices of the polylines must be not greater than $$$10^4$$$ by absolute value. Separate letters and integers with spaces. Check the sample output to clarify the format.

If there is more than one solution, any one of them will be accepted.

4
1 2 3 4 1 2 3 4

YES
3 U 1 R 4 D 1
5 D 1 L 2 U 3 R 6 D 2
5 D 2 R 6 U 3 L 2 D 1
3 D 1 R 4 U 1

4
1 2 3 4 1 3 2 4

NO

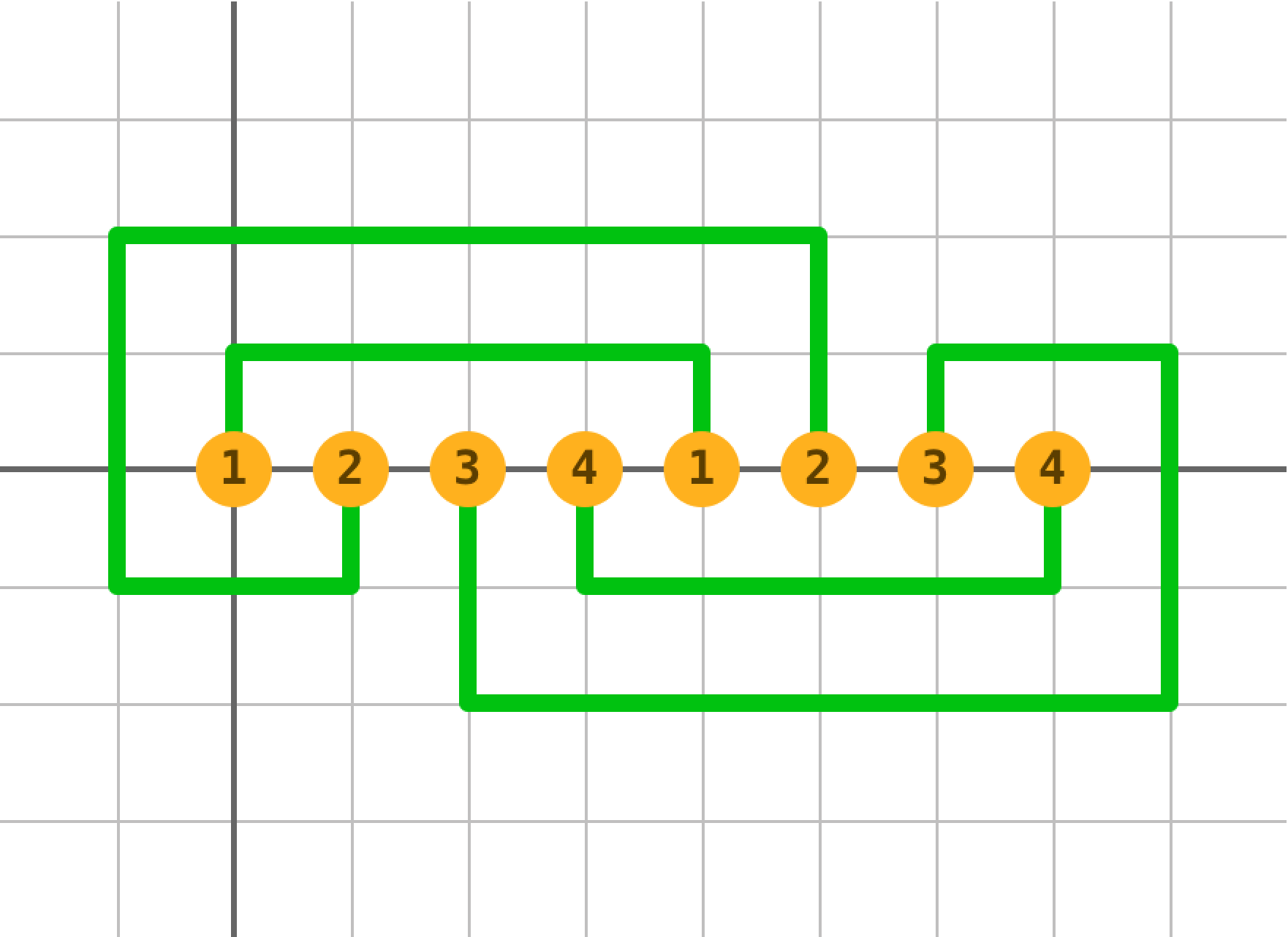
One of the possible circuits for sample 1 is shown at the picture. In sample 2, we cannot connect the pads so that the different tracks do not intersect.