407972: GYM102953 9 Subway System Spies
Description
You work for the CIA, and take the subway to work every day. The subway consists of $$$n$$$ stations, connected by $$$m$$$ lines. You live near station $$$a$$$, and work near station $$$b$$$. Each line consists of a specified route of $$$k_i$$$ stations (where each train goes either from the first to the last in order, or from the last to the first in order). You are guaranteed to be able to travel between any pair of stations by going on one or more subway lines.
Unfortunately, you've just received word that an enemy agent is hiding in one of the stations in the subway. You're not sure which one the enemy agent is hiding in, but you do know that they're going to stay in the same station for the whole day.
You still need to get to and from work, but you want to avoid ever being in the same station with the enemy agent. Thus, your task is to figure out, for each station, whether you can still travel from home to work (and back), if the enemy agent is in that station.
InputThe first line of input contains four space-separated integers $$$n$$$, $$$m$$$, $$$a$$$, and $$$b$$$ $$$(1 <= n, m <= 10^5)$$$, $$$(1 <= a, b <= n)$$$, $$$(1 <= \sum_{}{k_i} <= 10^5)$$$: the number of stations in the subway, the number of subway lines, the station that you live near, and the station that you work near, respectively.
Additionally, the subway system has at most 1000 "hub stations" (stations that more than one line go through).
The next $$$m$$$ line pairs each contain a single positive integer $$$k_i$$$, representing the number of stations that the line services, and a line consisting of the $$$k_i$$$ stations that the line services, in order.
OutputOutput a single binary string of length $$$n$$$, where a "1" character represents a station where, if the enemy agent was in the station, you could still go to work (and back), and a "0" character if not.
ScoringFull problem: 73 points
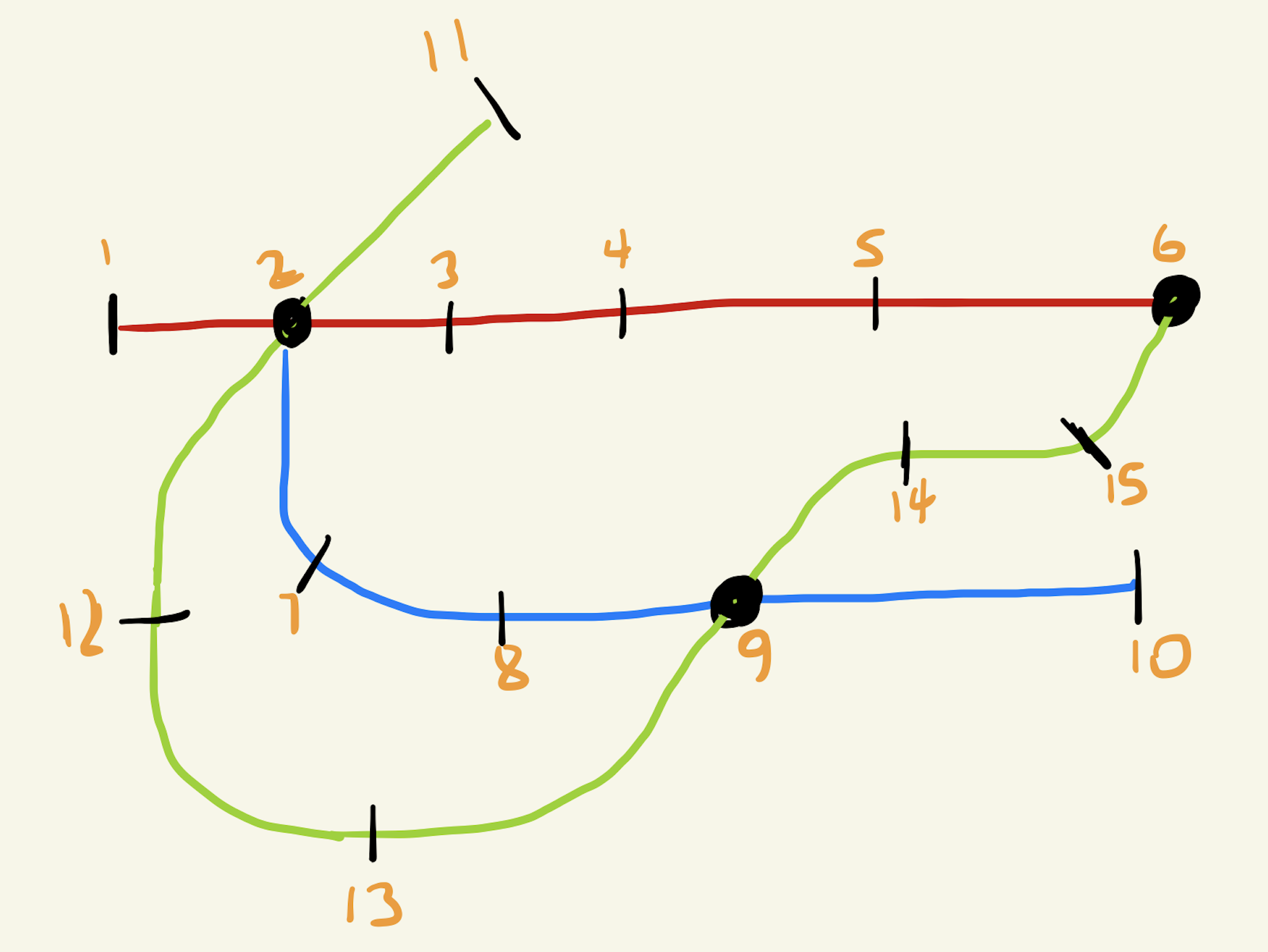
ExamplesInput15 3 1 10 6 1 2 3 4 5 6 5 2 7 8 9 10 8 11 2 12 13 9 14 15 6Output
001111110011111Input
18 3 3 5 8 1 2 3 18 4 5 6 7 7 10 9 8 2 11 12 13 7 15 14 9 4 13 16 17Output
110001111111111111Note
Here is a visual representation of the first example case: