407966: GYM102953 3 Taiga Tree
Description
You have a tree, or an undirected connected graph with no cycles, with $$$n$$$ vertices and $$$n - 1$$$ edges. Vertex 1 is the root.
You define a "leaf vertex" to be a vertex on the tree, other than the root, that is adjacent to exactly one branch vertex.
You also define a "branch vertex" to be a vertex on the tree other than the root, that is adjacent to exactly two other vertices, and adjacent to at least one leaf vertex.
You define a tree to be more of a "taiga tree" the more branch vertices that it has. Given a tree, figure out how many branch vertices it has.
InputThe first line of input contains a single positive integer $$$n$$$ $$$(1 <= n <= 10^5)$$$: the number of vertices on the tree.
The next $$$n - 1$$$ lines each contain two space-separated integers, each representing an edge on the tree.
OutputOutput a single positive integer: the number of branch vertices on the tree, as defined above.
ScoringFull problem: 15 points
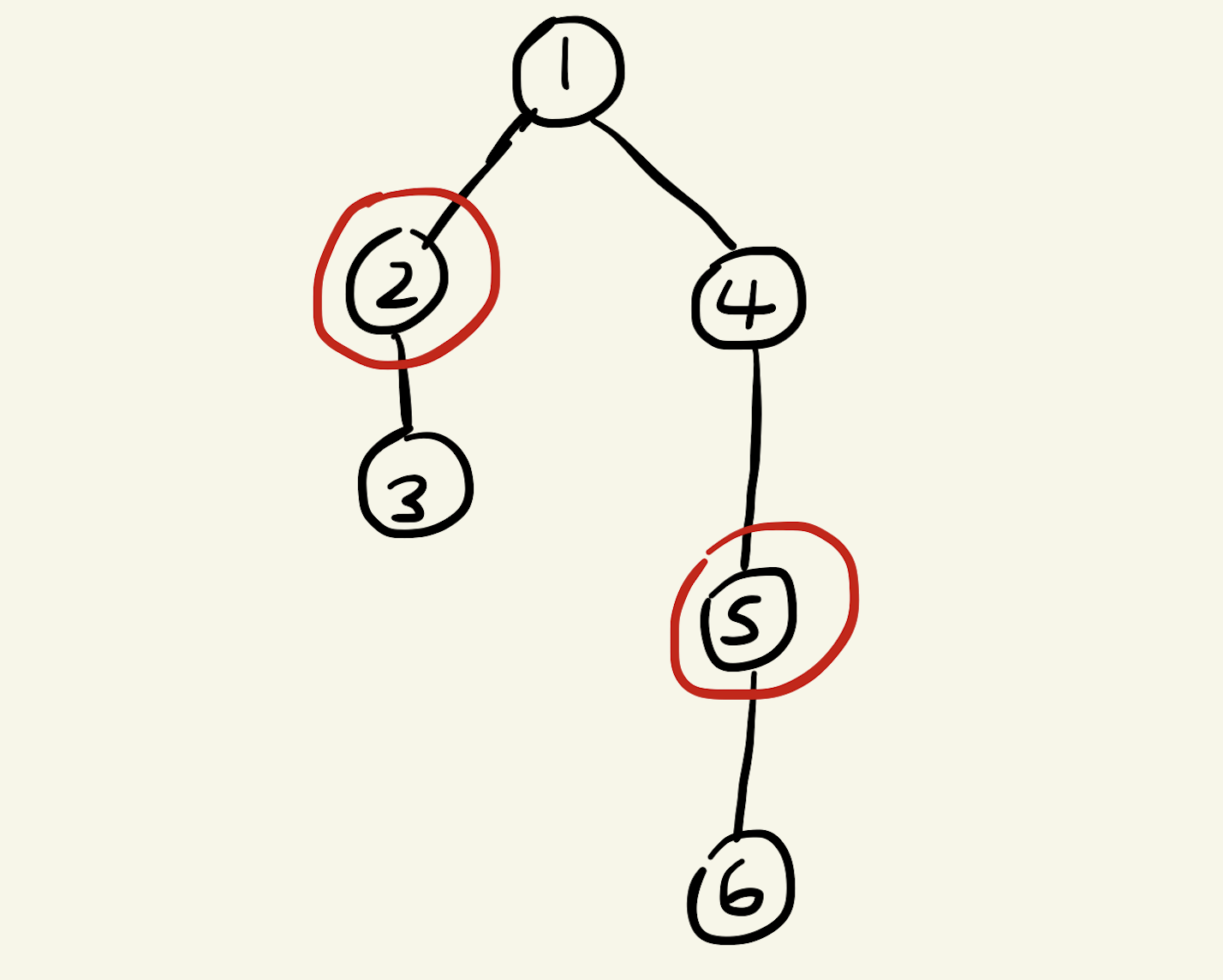
ExamplesInput6 1 2 2 3 1 4 4 5 5 6Output
2Input
8 1 2 2 3 1 4 4 5 5 6 6 7 6 8Output
1Note
Here is a visual representation of the first example case (the branch vertices are circled):