407925: GYM102944 B Bois Blanc

Bois Blanc is the French name for a special type of basswood. But if you are an expert on Michigan geography, you know that it is also a Michigan island at the northern end of Lake Huron. Of course, there are lots of basswood trees on the island. Unlike its famous and historical neighboring island – Mackinac Island – there are very few residents and visitors on Bois Blanc Island. It is known primarily for its lighthouses, which help guide ships entering and leaving the Mackinac Straits connecting Lake Huron and Lake Michigan.

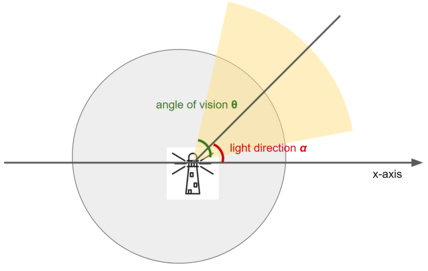
Let us suppose that Bois Blanc is perfectly circular (it's not, but it's difficult to come up with a problem for the real Bois Blanc shape). Designate a Cartesian coordinate system where the origin $$$(0,0)$$$ is at the center of the island and the island has radius 1. The State of Michigan has decided to build $$$N$$$ state-of-the-art lighthouses on the island, numbered $$$1,2,\ldots , N$$$. Lighthouse $$$i$$$ will be located at $$$(x_i, y_i)$$$ and have a specific light angle $$$\alpha_i$$$ and an angle of vision $$$\theta_i$$$ (see figure). Thus, the lighthouse illuminates the area between two rays, the first extending from $$$(x_i,y_i)$$$ at angle $$$\alpha_i-\theta_i/2$$$ and the second extending from $$$(x_i,y_i)$$$ at angle $$$\alpha_i+\theta_i/2$$$.

You have just been appointed Michigan Lighthouse Commissioner (congratulations!). You would like to ensure that these lighthouses altogether light up the entire periphery of the island (if all the lights are on) so that ships do not run ashore on the island. Island periphery is the circumference of the island. You are tasked to write a program that certifies this for you.

The first line in each input file contains an integer $$$N$$$ ($$$1\le N\le 100$$$), indicating the number of lighthouses on the island. In each of the next $$$N$$$ lines, there are four real numbers $$$x_i, y_i, \alpha_i, \theta_i$$$ ($$$x_i^2+y_i^2 < 1$$$; $$$0\le \alpha_i < 2\pi$$$; $$$0 < \theta_i < \pi$$$). Angles are given in radians.

The input is guaranteed that if you move the coordinates and angles of a lighthouse by $$$\pm 10^{-4}$$$, the answer will not change.

For each test case, output YES if all lighthouses altogether light up the periphery of the island, and output NO otherwise.

4
0.2 0.2 0.785398 1.570796
-0.2 0.2 2.356194 1.570796
-0.2 -0.2 3.926990 1.570796
0.2 -0.2 5.497787 1.570796

NO

4
0.3 -0.2 0.785398 1.570796
0.2 0.3 2.356194 1.570796
-0.3 0.2 3.926990 1.570796
-0.2 -0.3 5.497787 1.570796

NO

4
0.2 -0.3 0.785398 1.570796
0.3 0.2 2.356194 1.570796
-0.2 0.3 3.926990 1.570796
-0.3 -0.2 5.497787 1.570796

YES

8
0.160778 -0.455910 2.270371 2.260020
-0.059877 -0.152423 2.615438 2.349560
0.092217 -0.908759 3.937581 2.103347
0.634763 0.439841 0.246451 0.232265
-0.291208 0.939505 6.245182 2.622931
0.005957 0.114427 1.133582 1.039842
-0.303909 0.652162 4.819728 0.999183
-0.625112 -0.292457 5.316244 0.593612

YES