407900: GYM102920 J Switches

Alice, who loves to travel, got to stay at a very interesting hotel. Every guest who wishes to stay at the hotel should solve an interesting quiz about the lights installed in the room where they will be staying. The front desk of the hotel gives each guest an information on the lights installed in the room where they are staying and the switches connected to the lights. According to the information, one or more lights are connected to one switch, and each light is connected to one or more switches.

There are $$$N$$$ lights and $$$N$$$ switches in the room where Alice will be staying. What is interesting is that when Alice makes a switch on, not only one light is turned on, but several lights are turned on at the same time. Also, making another switch on while one or more switches are already on may turn off some lights that are already turned on. Fortunately, when all the switches are off, all the lights are off as well.

Figure J.1 is an example of the information Alice received from the front desk of the hotel, where $$$N = 5$$$.

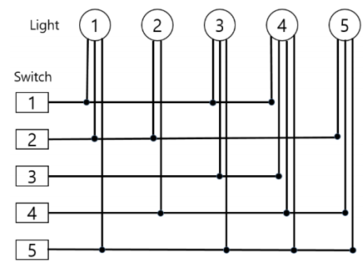
Figure J.1

To figure out how each light is affected by the switches, Alice experiments as follows. First, each light is numbered and the switches are also numbered so that they could be identified. She makes all the switches off initially. Then, she checks which lights are turned on by making only the switch #1 on. After that she makes switch #1 off and switch #2 on to check which lights are turned on. Again, she makes switch #2 off and switch #3 on, and so on. She repeats this to check which lights are turned on by each switch.

Then, she makes two or more switches on to find what rules exist. As a result, it is found that each light is toggled by the switches that are connected to it. This rule can be stated as follows:

• A light is turned on (off) when the number of switches, which are connected to it and are on state, is odd (even).

For example, consider the connection information shown in Figure J.1 and focus on how light #1 operates. The light #1 turns on by making each of the switches #1, #2 and #5 on. If she makes switch #1 on while all the other switches (i.e., switch #2 and #5) are off, light #1 turns on. And, if she additionally makes switch #2 on, light #1 turns off. If she additionally makes switch #5 on (that is, all the three switches are on), light #1 turns on again. While operating such switches, the state of other lights may also change.

Alice wonders if for each light, it is possible to turn it on and the rest of the lights off by operating some switches.

Given the connection information between switches and lights, write a program to help Alice. In other words, your program should tell whether for each light, it is possible to turn it on and the rest of the lights off by operating some switches.

Your program is to read from standard input. An integer $$$N$$$ ($$$3 \leq N \leq 500$$$) is given in the first line. Each of the following $$$N$$$ line contains $$$N$$$ integers of 0's and 1's separated by a single space. The numbers in the $$$i$$$-th ($$$1 \leq i \leq N$$$) line represent which lights are connected to the $$$i$$$-th switch. If the $$$k$$$-th ($$$1 \leq k \leq N$$$) value in the $$$i$$$-th line is 1, it means the $$$k$$$-th light is connected to the $$$i$$$-th switch; 0 means it is not connected.

Your program is to write to standard output. If for every light, it is possible to turn it on and the rest of the lights off by operating some switches, print the switch numbers in increasing order that should be on. Otherwise, print -1 as shown in the following samples. If your output is not -1, the switch numbers in the $$$k$$$-th line should be those that make the $$$k$$$-th light on. If there are more than one correct answers print any of them.

4
1 0 1 0
0 1 0 1
0 1 1 1
1 1 0 0

1 2 3 
1 2 3 4 
2 3 
1 3 4 

4
1 1 1 0
0 1 0 1
1 0 0 1
0 1 1 1

-1

5
1 0 1 1 0
1 1 0 0 1
0 0 1 1 0
0 1 0 1 1
1 0 1 1 1

1 3 
2 3 5 
1 2 4 
1 2 3 4 
1 5