407898: GYM102920 H Needle

The "needle" is a legendary assassin who lives in the North Kingdom. As you know, the needle is very thin and long. More than anything, it is deadly sharp. The king of the North Kingdom is obsessed with the idea that the needle might kill him by stabbing countless times. The king issued an emergency order to arrest the needle. So, the needle decided to escape to the South Kingdom.

As shown in the figure below, the border between two kingdoms consists of three horizontal barriers (line segments), each of which has one or more infinitesimally small holes inside. (The holes are marked as x in the figure.) Three barriers have the same length and are aligned vertically as in the figure. The upper barrier is one unit above the middle barrier, which is one unit above the lower barrier. Two kingdoms are surrounded by impenetrable outer wall. Each kingdom also has a very large territory so that the needle can move (translate or rotate) freely inside the kingdom. The needle is at least twice as long as the barriers. The needle is rigid, i.e., not bendable, and has zero-thickness, so it can pass the holes freely, but cannot drill any other part of the barriers than the holes.

The only way from the Northern Kingdom to the Southern Kingdom is through three holes, one from each of the three barriers, at the same time. In other words, the needle can pass the border only through three holes, exactly one from each barrier, which are aligned on a line. The border in the figure has two possible escape passages from the north to the south.

For this pity assassin, write a program to tell how many possible escape passages from the North Kingdom to the South Kingdom are available.

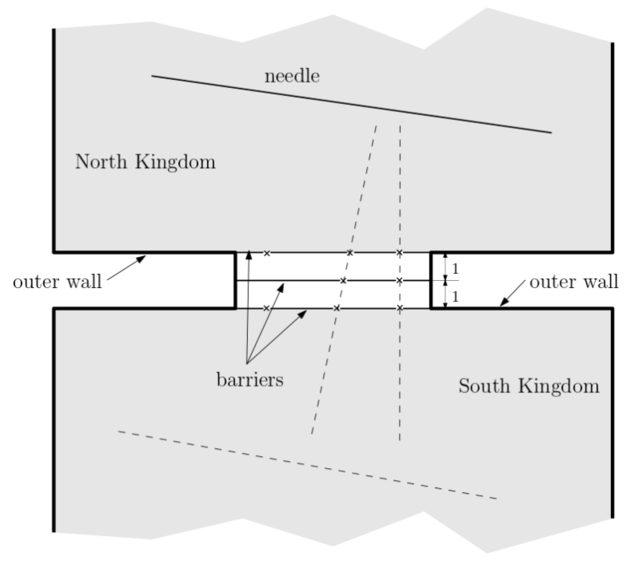
Your program is to read from standard input. The input consists of six lines. The first line contains a positive integer $$$n_u$$$ representing the number of holes of the upper barrier. The second line contains $$$n_u$$$ integers separated by a space that represent the $$$x$$$-coordinates of the holes. The third and fourth lines are for the middle barrier, each containing $$$n_m$$$, the number of holes of the middle barrier, and $$$n_m$$$ $$$x$$$-coodinates of the holes. The fifth and sixth lines are for the lower barrier, each containing $$$n_l$$$, the number of holes of the lower barrier, and $$$n_l$$$ $$$x$$$-coodinates of the holes. $$$1 \leq n_u, n_m, n_l \leq 50,000$$$ and all $$$x$$$-coordinates of the holes are integers between $$$−30,000$$$ and $$$30,000$$$. Holes of each barrier have all distinct $$$x$$$-coordinates.

Your program is to write to standard output. Print exactly one line. The line should contain a nonnegative integer representing the number of all possible passages from the north to the south.

1
1
1
2
1
1

0

3
4 -3 2
2
4 1
3
-3 4 0

2

3
-1 1 0
3
0 1 -1
3
0 -1 1

5