407779: GYM102892 8 Maximum Donut
Description
You have an $$$n$$$ by $$$n$$$ 2D grid of integers ranging from $$$-100$$$ to $$$100$$$. You define a donut as a ring of numbers in the 2D grid, with a width of one. For example, this is an example of a donut (highlighted in green):
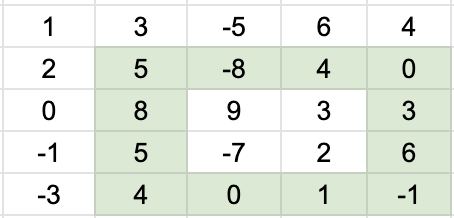
Note that a donut must include a "hole", i.e. a $$$2$$$x$$$2$$$ square is not considered a donut. Note also that a donut does not have to be in a square shape.
The value of a donut is defined as the sum of the numbers that it contains. For example, the donut pictured above has a value of 27. Given an $$$n$$$ by $$$n$$$ 2D grid, your task is to find the donut with the maximum value.
InputThe first line of input contains a single positive integer $$$n$$$ ($$$n <= 400$$$): the width and height of the grid.
The next $$$n$$$ lines each contain $$$n$$$ space-separated integers, representing the elements of the grid. Each element will range from $$$-100$$$ to $$$100$$$, inclusive
OutputOutput the value of the maximum donut in the 2D grid.
ScoringSubtask 1 (13 points): $$$n <= 80$$$
Subtask 2 (34 points): no further constraints
ExamplesInput5 1 3 -5 6 4 2 5 -8 4 0 0 8 9 3 3 -1 5 -7 2 6 -3 4 0 1 -1Output
39Input
5 13 15 -2 -3 -5 14 18 -5 -8 -10 -2 -2 1 -1 2 4 -1 0 5 -6 -2 -1 1 -1 0Output
37Input
3 -1 -2 -3 -4 -5 -6 -7 -8 -9Output
-40