407636: GYM102861 O Venusian Shuttle

The Human Colony at Venus is thriving! Here, the main form of public transportation is the Venusian Shuttle: it is a round flying disc, with windows and seats all around its border. In this shuttle, all the seats are window seats. And people are not allowed to move from one seat to another. So once someone chooses a seat, they must remain there until they leave the shuttle.

Even though it is a fully autonomous vehicle, every shuttle operates with an engineer on board, to handle any unexpected problems. You are Shuttle 1C9C's engineer, and you spend most of your work shift reading books. The problem is that you hate being exposed to the sun. Therefore, you want to choose a place to sit that minimizes the total amount of sunlight you take along your entire work shift.

The colony is represented by the Cartesian plane, where the $$$X$$$ axis points east and the $$$Y$$$ axis points north. The days at Venus are very long (in fact, longer than the year!), so you can assume that the sun always shines from the east direction. That is, the sunlight always travels west, in the negative $$$X$$$ direction.

See the figure below. The more your window is turned east, the more sunlight you're exposed to. But if your window is turned west, you're not exposed to the sun at all.

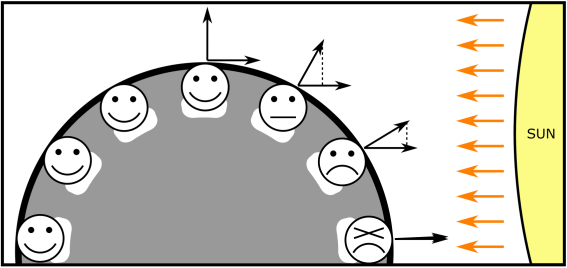
Formally, suppose the vector $$$(D_x, D_y)$$$ represents the direction faced by your window. Note that you only get any sunlight if $$$D_x > 0$$$. And let $$$\theta$$$ be the angle between the vectors $$$(D_x, D_y)$$$ and $$$(1, 0)$$$ (a vector pointing directly towards the sun). If $$$\cos(\theta) \le 0$$$ then you don't get any sunlight. Otherwise, you receive $$$\cos(\theta)$$$ units of sunlight per second.

The shuttle route consists of a sequence of stations around the colony. The shuttle starts the work shift at the first station, visits all stations in order, and then returns to the first one.

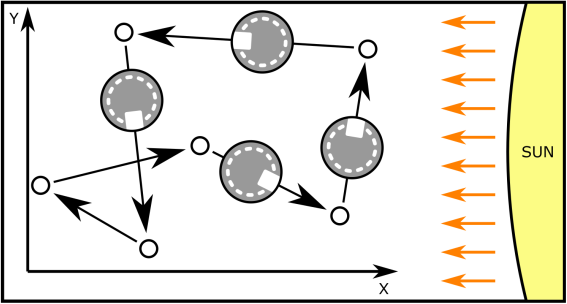
The shuttle always follows a straight line when going from one station to another, moving with constant speed of one meter per second. And although the shuttle is round, it has a "front side": this side is always facing the direction it is moving forward, and the shuttle rotates accordingly when it changes direction at the stations.

You may ignore time spent turning the shuttle around, picking up or dropping off passengers.

The first input line contains a single integer $$$N$$$, the number of stations visited during the shuttle's route.

Then, $$$N$$$ lines follow, each line containing the coordinates $$$X$$$ and $$$Y$$$ of a station, separated by a single space.

The stations are given in the order they are visited.

Any station may be visited more than once in the route.

Any two consecutive stations are distinct, as well as the last and first stations.

All coordinates are given in meters.

$$$2 \le N \le 100000$$$.

The coordinates of each station are integers in the interval $$$-10000 \le X, Y \le 10000$$$.

The output consists of a single line with a real number, the minimum total amount of sunlight you can take in a single tour around the shuttle route. Your answer should have exactly two digits after the decimal point.

3
2 5
17 5
11 11

6.00

4
3 0
3 6
6 3
0 3

4.24

4
3 2
1 1
-3 -1
-1 0

0.00