407634: GYM102861 M Machine Gun

Fulanito plays an old-school arcade game. In the game, he can place a machine gun anywhere within his base, which contains all $$$(x, y)$$$ points with $$$x < 0$$$. There are $$$N$$$ enemies on the battlefield. The $$$i$$$-th enemy $$$(1 \le i \le N)$$$ is at position $$$(x_i, y_i)$$$ with $$$x_i > 0$$$. All these positions are given in advance.

A machine gun at $$$(x_m, y_m)$$$ covers an angle of vision to the right, centered on the line $$$y = y_m$$$, and whose borders are given by lines $$$y = y_m \pm \frac{x-x_m}{2}$$$. When placed, it kills all enemies within such angle, including its border lines.

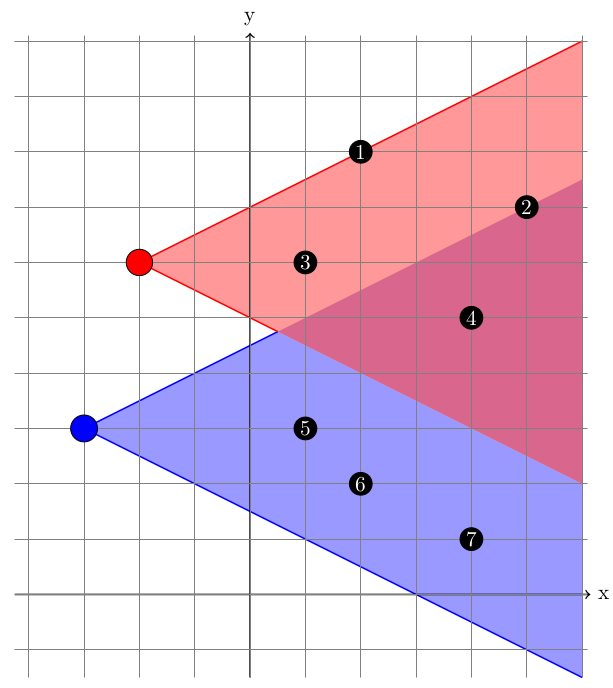Figure 1: Pictorial representation of the sample input

The scoring system used by this videogame is extremely awkward: many believe that it was in fact a horrible bug by the game developers, who then proceeded to just yell "it's not a bug, it's a feature!" to anyone asking about it. Specifically, the score achieved by a certain placement of the machine gun is calculated by executing the following steps:

• Take the ids ($$$i$$$ between 1 and $$$N$$$) of all the enemies that it kills.
• Sort all those ids in increasing order.
• Let the sorted values be $$$i_0 < i_1 < \dots < i_{k-1}$$$
• Compute the score as $$$\left(\sum^{k-1}_{j=0} i_j \cdot 5782344^j\right)\mod (10^9 + 7)$$$
• Note: A machine gun that kills no enemies gets a score of exactly $$$0$$$ points.

To get better at this game, Fulanito is going to ask you $$$q$$$ questions: each question asks the score that would be achieved by placing the machine gun at a certain $$$(x_m, y_m)$$$.

To make the problem more challenging, each $$$(x_m, y_m)$$$ is not given directly. Instead, values $$$a$$$ and $$$b$$$ are given, such that $$$x_m = -1 - \left( (p + a) \mod (10^9 + 7) \right)$$$ and $$$y_m = (p + b)\mod (10^9 + 7)$$$, where $$$p$$$ is the answer to the previous query ($$$p = 0$$$ when processing the first query).

NOTE: It is guaranteed that in total, taking all queries together, the number of killed enemies is at most $$$10^6$$$.

$$$1 \le x_i, y_i \le 10^9$$$.

$$$1 \le N, q \le 10^5$$$.

$$$0 \le a, b < 10^9 + 7$$$.

The first line contains the two integers $$$N$$$, $$$q$$$.

The next $$$N$$$ lines contains two integers each: $$$x_i$$$ and $$$y_i$$$.

The next $$$q$$$ lines contains two integers each: The values $$$a$$$ and $$$b$$$ that specify each query as explained in the problem statement.

For each query, output a single line with a single integer containing the answer to that query.

7 2
2 8
5 7
1 6
4 5
1 3
2 2
4 1
2 3
373785639 373785644

626214369
981053491