407575: GYM102832 C Quantum Geometry

Once there was a spiritual guy, who wanted to meet his best friend as soon as possible. Both he and his friend were on an Euclidean plane. He started his trip from $$$(0, 0)$$$, and his friend was located at $$$(L, 0)$$$.

If everything had been normal, he would reach his destination by walking $$$L$$$ meters, straight from $$$(0, 0)$$$ to $$$(L, 0)$$$. However, the region around was influenced by a mysterious force, which might be blamed on the $$$n$$$ magic towers around.

Every midnight, three towers were chosen by the mysterious force. High walls would appear on the boundary of the triangle formed by them as vertices, and would stay there until the next midnight. The walls were high enough to block sight, causing the spiritual guy unable to learn what was behind the wall. In other words, if the spiritual guy could only see one wall, any tower blocked by the wall, from his perspective, might be chosen as the remaining third tower. The spiritual guy travelled so fast that he could arrive where his friend were within one day. Therefore, you may assume the $$$3$$$ towers chosen remained unchanged during his trip. While travelling, he could gradually learn about the unknown area from his new perspective. Fortunately, he had so good a memory and a sense of direction that he knew where the $$$n$$$ towers and his destination were even if they were blocked by the wall, and could remember any situation as long as he was once able to see it. The spiritual guy was a pessimist, and would choose the shortest strategy in the worst case.

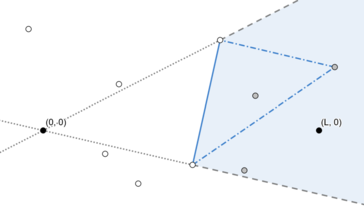
Example: The spiritual guy knew where the three grey towers and his destination were, but could not determine which one of the three grey towers was chosen when he set off.

If the spiritual guy could see all three chosen towers when departing, choosing a shortest path was no difficulty to him, so he came to you to verify his strategy where he could only see two chosen towers when he set off. He had designed several situations, and you are expected to tell him how much distance he needed to travel in the worst case, so that he could check his own answer.

The first line contains three integers $$$n$$$, $$$L$$$ and $$$q$$$ ($$$3 \leq n \leq 3 \times 10^3, 2 \leq L \leq 10^8$$$, $$$1 \leq q \leq 3 \times 10^5$$$), where $$$q$$$ represents the number of situations the spiritual guy had designed.

Each of the next $$$n$$$ lines contains two integers $$$x$$$ and $$$y$$$ ($$$|x| \leq 10^8, |y| \leq 10^8$$$), indicating that there was a tower at $$$(x, y)$$$.

Each of the next $$$q$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \leq u < v \leq n$$$), indicating the situation that only the $$$u$$$-th and $$$v$$$-th towers in the above input could be seen when the spiritual guy set off. It is guaranteed that there was at least one tower blocked by the wall connecting these two towers.

It is also guaranteed that neither the starting point nor the destination might be surrounded by the walls no matter how the mysterious force chose towers. In addition, you may assume that no line would pass at least three of the towers, the starting point and the destination.

For each situation, print on a line the minimum distance needed to be travelled in the worst case.

Your answer is considered correct if its absolute or relative error does not exceed $$$10^{-9}$$$.

Formally, let your answer be $$$a$$$, and the jury's answer be $$$b$$$. Your answer is accepted if and only if $$$\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-9}$$$.

5 5 2
1 2
2 2
4 1
1 -2
3 -2
1 4
1 3

6.841619252964
5.000000000000

For the first situation in the example, the spiritual guy would go straight to $$$(1, 2)$$$ to have a look of what was behind the first wall. Only at the moment he arrived at $$$(1, 2)$$$ could he get some new information, and at that moment the worst case was that $$$(2, 2)$$$ was chosen to be the third tower. Another strategy was to go to $$$(1, -2)$$$ after departing, the worst case was that $$$(3, -2)$$$ was chosen, resulting a longer distance. You may prove that all other strategies also had a worse result.

For the second situation in the example, $$$(2, 2)$$$ was the only choice of the third tower. The spiritual guy could walk straight from $$$(0, 0)$$$ to $$$(5, 0)$$$.