407452: GYM102798 F Skeleton Dynamization

The skeleton data has been widely used in computer vision tasks such as action recognition. In the skeleton model, the human body is represented by a set of body joints interconnected by bones. This naturally forms an undirected graph model: vertices are joints and edges are bones.

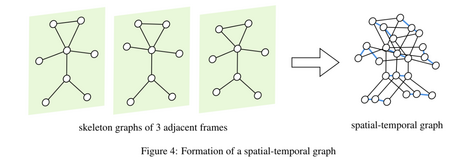
To incorporate the dynamics of the skeletons in a video, we may keep track of the joints across the frames and build a spatial-temporal graph for the video. The spatial-temporal graph consists of the skeleton graphs of every frame, with additional inter-frame edges connecting the same joints in two adjacent frames. Note that the skeleton graph should keep the same in all frames of the video. The following picture exhibits how a spatial-temporal graph is formed.

Your task is to reverse-engineer a spatial-temporal graph. Formally, you should assign a pair of integers $$$(f_v, s_v)$$$ to every vertex $$$v$$$ of the graph, where $$$f_v$$$ is the frame number and $$$s_v$$$ is the index of the joint. Let $$$T, S$$$ denote the number of frames and the number of joints, respectively, then your labeling must simultaneously satisfy the following conditions:

• for every $$$1 \leq t \leq T$$$ and $$$1 \leq i \leq S$$$, exactly one vertex is labeled $$$(t, i)$$$;
• there is an edge between vertices labeled $$$(t, i)$$$ and $$$(t+1, i)$$$ for every $$$1 \leq t < T$$$ and $$$1 \leq i \leq S$$$; there are no inter-frame edges other than those mentioned before;
• for every $$$1 \leq t_1 < t_2 \leq T$$$ and $$$1 \leq i < j \leq S$$$, there is an edge between vertices labeled $$$(t_1, i)$$$ and $$$(t_1, j)$$$ if and only if so between $$$(t_2, i)$$$ and $$$(t_2, j)$$$.

The first line of the input consists of two integers $$$n, m$$$ $$$(1 \leq n \leq 100\,000, 0 \leq m \leq 200\,000)$$$, denoting the number of vertices and edges in the given spatial-temporal graph respectively. The vertices of the graph are indexed $$$1$$$ through $$$n$$$.

Each of the remaining $$$m$$$ lines of the input contains two integers $$$u, v$$$ $$$(1 \leq u, v \leq n, u \neq v)$$$, denoting an undirected edge connecting vertices indexed $$$u$$$ and $$$v$$$. Each pair of vertices is connected by at most one edge. The input graph is guaranteed to be connected.

Print two integers $$$T, S$$$ in the first line of your output, denoting the number of frames and the number of joints, respectively. Then print $$$T$$$ lines, each containing $$$S$$$ integers; the $$$s$$$-th integer of the $$$t$$$-th line is the index of the vertex labeled $$$(t, s)$$$.

If multiple valid labelings exist, print the one with the maximum number of frames. If there are still multiple, any one is acceptable.

12 20
5 12
6 10
8 1
11 3
5 1
12 4
12 2
11 8
2 8
6 4
7 11
9 1
8 10
9 6
4 1
2 5
10 3
7 2
8 4
9 10

3 4
3 6 9 10
11 4 1 8
7 12 5 2

3 3
1 2
2 3
3 1

1 3
1 2 3

4 3
1 2
2 3
4 3

4 1
1
2
3
4