406961: GYM102625 G Secret Society and a Certain Someone

For some unknown (read obvious) reason, most of the students of IIT(ISM) hate a certain someone who is (in)famous for his greeting. Some students took that hate to a different level by forming a secret society. Their society has a network consisting of $$$\textbf{n}$$$ secret offices spread across the campus, numbered $$$\textbf{1}$$$ through $$$\textbf{n}$$$.

There are $$$\textbf{n-1}$$$ secret passages, where each passage connects two offices. The passages are constructed such that every office is reachable from every other office by using some passages. The passages also have a level of security attributed to them. The members of this society only discuss in one of their secret offices. To make things fair between every office, a meeting takes place at each office exactly once.

To attend a meeting to be held at office $$$\textbf{u}$$$, representatives from every other vertex will reach $$$\textbf{u}$$$ by following the shortest path to $$$\textbf{u}$$$. The representatives are smart, so they will hide the information gained in a meeting in the passage with highest level of security on their way back to their respective offices. If there are multiple such passages with highest security level, a copy of the information will be hidden in each passage.

The leader of the society wants a quick overview of all the meetings (one meeting held at each office). Since he is busy spending most of his time protecting the society from that certain someone, he only views informations in the passages where maximum number of informations ( copies are also genuine informations) are hidden. He considers those passages $$$\textbf{most informative passages}$$$. Since, you are also a member (don't worry if you are not a member yet, the legend of IIT(ISM) says that you'll willingly join soon), help your leader find the number of informations hidden in the most informative passage and also the number of such passages.

The first line of the input consists of a single integer $$$\textbf{n}$$$ (2 $$$\leq$$$ $$$n$$$ $$$\leq$$$ 2$$$\cdot$$$10$$$^{5}$$$), the number of secret offices.

Each of the next $$$\textbf{n-1}$$$ lines consists of 3 integers $$$\textbf{u}$$$, $$$\textbf{v}$$$ and $$$\textbf{w}$$$, which means there is a secret passage between offices numbered $$$u$$$ and $$$v$$$ (1 $$$\leq$$$ $$$u$$$,$$$v$$$ $$$\leq$$$ $$$n$$$ and $$$u$$$ $$$\neq$$$ $$$v$$$) and has a security level $$$w$$$ (1 $$$\leq$$$ $$$w$$$ $$$\leq$$$ 10$$$^{9}$$$).

Output consists of two lines.

In the first line print two integers $$$\textbf{m}$$$ and $$$\textbf{k}$$$, number of informations hidden in the most informative passage and the number of such passages respectively.

In the second line print a list of $$$\textbf{k}$$$ integers which are the most informative passages $$$\textbf{sorted}$$$ in increasing order, the passages are numbered $$$\textbf{1}$$$ through $$$\textbf{n-1}$$$ in the order they appear in the input.

3
2 1 3
3 1 1

4 1
1 

5
2 1 3
4 3 1
5 4 1
2 3 1

8 2
1 2 

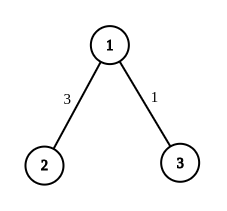
Information will be hidden in passage $$$(1,2)$$$ $$$4$$$ times. Once for meeting at $$$3$$$(by representative of $$$2$$$), once for meeting at $$$1$$$(by representative of 2), and twice for meeting at $$$2$$$(by representatives of both $$$1$$$ and $$$2$$$). Since this passage appears first in the input it is numbered $$$1$$$.

For passage $$$(1,3)$$$, infromation is hidden twice. Once for meeting at $$$1$$$(by representative of $$$3$$$) and once for meeting at $$$3$$$(by representative of $$$1$$$). This edge is numbered $$$2$$$.

Since more information is hidden in passage numbered $$$1$$$, it is the most informative passage and it has $$$4$$$ hidden information.

In the second example, both the passages $$$(1,2)$$$ and $$$(3,4)$$$ have maximum number of hidden information($$$8$$$). Hence, both are considered most informative passages.