406803: GYM102562 D Cupidus the Cupidon
Description
In 2020, due to $$$issues$$$ worldwide, $$$Cupidonus$$$ moved his tutoring program online. For a small reasonable amount (4000 - 5000 Euros) he can teach you the ways of the $$$cupid$$$, so you will be able to become a $$$Cupidon$$$. Of course inferior to $$$Cupidonus$$$.
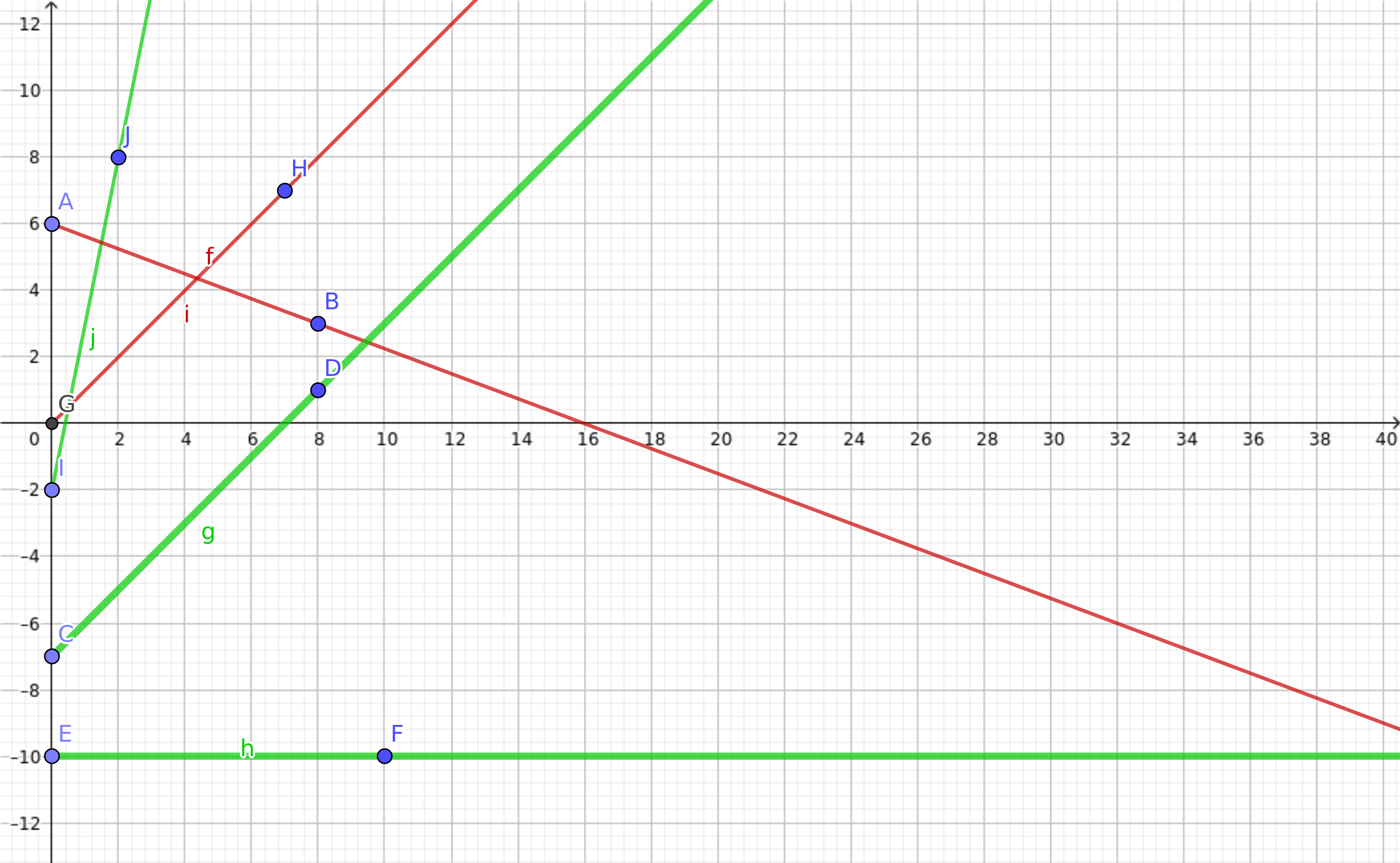
As a result $$$N$$$ smarties registered for his program. Since $$$Cupidonus$$$ is really busy, he decided to organize a test in order to select the right candidate in one go. As a result, he aligned all the smarties on the $$$OY$$$ axis and asked each of them to shoot an arrow in the semiplane with $$$x > 0$$$. $$$Cupidonus$$$ will select the maximum number of smarties such that any two trajectories of their arrows do $$$NOT$$$ intersect.
$$$Cupidonus$$$ asked you to supervise the test and tell him how many candidates will be selected.
InputThe first line of the input will contain the number of test cases $$$T$$$ ($$$1 \leq T \leq 100000$$$).
The first line of each test case will be the number $$$N$$$ ($$$1 \leq N \leq 10^5$$$), the number of smarties who registered to become a $$$Cupidon$$$.
The following $$$N$$$ lines of each test case will each contain $$$3$$$ integers $$$a_i$$$, $$$x_i$$$, $$$y_i$$$ ($$$-2^{52} \leq a_i, y_i \leq 2^{52}$$$, $$$1 \leq x_i \leq 2^{52}$$$, $$$1 \leq i \leq N$$$), the position of the $$$i$$$th smartie on the $$$OY$$$ axis and the coordinates where his arrow landed. All $$$a_i$$$ are pairwise distinct.
It is guaranteed that the sum of $$$N$$$ over all test cases does not exceed $$$500000$$$.
OutputThe output should contain $$$T$$$ lines, each containing the answer to the corresponding test case.
ExampleInput2 5 6 8 3 -7 8 1 -10 10 -10 0 7 7 -2 2 8 5 2 6 -4 6 1 6 -6 6 -9 -5 7 1 4 4 -3Output
3 2Note
For the first example we can choose the smarties with indexes: 2, 3, 5. See image below.