406770: GYM102536 I Glory to Algotzka

Congratulations, comrade! You have won the labor ticket.

Report to the Auditing and Census Ministry (ACM).

Company Olympichia has been infiltrated by capitalists.

Algotzkan government needs to determine severity.

Your orders: evaluate compromisation for all inquiries.

Glory to Algotzka.

The structure of Company Olympichia is best described as a rooted tree. $$$n$$$ employee details have been given. Each detail includes which employee is the superior of another, and if they are suspected capitalist spies, or patriotic socialist comrades.

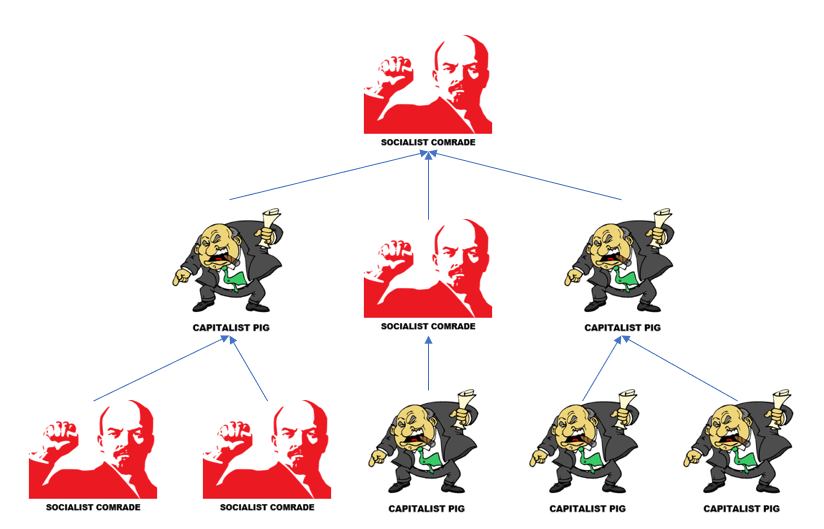
The Ministry has been given $$$q$$$ inquiries. Each inquiry contains an employee $$$i$$$ to be investigated, number of filthy capitalist spies $$$c$$$ and number of upstanding socialist comrades $$$s$$$.

You are required to give report on chain of command for each inquiry. A valid chain of command for employee $$$i$$$ is any connected subgraph that is rooted at $$$i$$$.

If there exists a valid chain of command with exactly $$$c$$$ cowardly capitalist spies and $$$s$$$ peerless socialist comrades, then company is compromised. Otherwise, it is not compromised.

Photos taken from https://munkahelyiterror.blog.hu/2012/07/17/lekurvazott_es_fizikailag_bantalmazott_az_elelmezes_vezeto and https://ycl.org.uk/ licensed under https://creativecommons.org/licenses/by-nc-nd/3.0/

There is one test case for each input file.

Input starts with one line containing two space-separated integers $$$n$$$ and $$$q$$$, the number of employees and inquiries respectively. The employees are numbered from $$$1$$$ to $$$n$$$.

The second line contains a list of $$$n$$$ space-separated integers $$$E_1, E_2, \ldots, E_n$$$: the Olympichia employee details given to you by the government of Algotzka. The $$$j$$$th number $$$E_j$$$ in the list corresponds to the employee number which is the direct superior of the one in the list. The first number in this list $$$E_1$$$ (counting starts at $$$1$$$) is always the root node for the entire company; we will denote this by having $$$E_1 = 0$$$.

The third line contains a string of length $$$n$$$, $$$A = A_1A_2\ldots A_n$$$ denoting the affiliations of the Olympichia employees described above. The $$$j$$$th character, $$$A_j$$$, can only be one from the following:

1. C: $$$j$$$th employee is a dastardly capitalist.
2. S: $$$j$$$th employee is a unwavering socialist comrade.

Then $$$q$$$ lines follow. Each line contains three space-separated integers $$$i$$$, $$$c$$$, and $$$s$$$. This represents each inquiry made by the Algotzkan government.

Constraints

• $$$1 \le n \le 10000$$$
• $$$1 \le q \le 200000$$$
• $$$1 \le i \le n$$$
• $$$0 \le c, s \le 10000$$$
• $$$c + s > 0$$$
• The length of $$$A$$$ is $$$n$$$.
• Each $$$A_j$$$ is either C or S.
• $$$E_1 = 0$$$
• $$$1 \le E_j < j$$$ for $$$1 < j \le n$$$

Output one line for each inquiry, containing the result of the investigation (without the quotes):

• "COMPROMISED" If there exists a connected subgraph in the subtree rooted at employee $$$i$$$ with exactly $$$c$$$ capitalists and exactly $$$s$$$ socialists.
• "NOT COMPROMISED" If no such connected subgraph exists.

5 3
0 1 2 3 4
CSCSC
1 3 2
1 2 2
2 2 1

COMPROMISED
COMPROMISED
NOT COMPROMISED