406758: GYM102535 O 1\% Genius

It's just another day at National Corps of Intelligence Services (NCIS), the country's biggest and most powerful espionage organization. You're enjoying your favorite drink as you read through some top secret files and type away at your computer desk to finish your report for the previous mission. Everything seems normal, but then...

"No way, I'm getting hacked!", your colleague suddenly exclaims.

"A port scan?", you ask her.

"No. No, this is major. They've already burned through the NCIS public firewall," she replies, frantically typing at her keyboard.

"Well, isolate the node and dump it on the other side of the router,'' you suggest to her.

"I'm trying! It's moving too fast."

As she says this, you notice the hacker's progress on her screen. Multiple pictures of random cats keep on popping up. Several memes from Gag-Olympics show up. It looks like someone on Hacker Typer, but you are sure that this isn't a prank this time.

Not being the type to just sit back and watch your precious colleague suffer, you heroically join her on the keyboard as she continues to type away to beat the hacker. Together, you can beat the hacker, you say.

As soon as you did this, more things popped up on the screen. CAPTCHAs? No, IQ tests! "99% of the population can't solve this," it says on the screen.

"Which cup will be filled first?"

It's a very tough and difficult logic puzzle where cups are connected via tubes, and water pours in from one of the cups. Thankfully, you always knew that you were part of that special 1% of the population that can solve this puzzle, and proceed to type with your colleague to beat the hacker.

In fact, instead of just knowing which cup will be filled first, you set yourself a more ambitious goal: to know precisely where the water is at any moment in time. But you're not willing to simulate the physics of flowing water accurately. Instead, you decide on the following approximation:

• The diagram is modeled as an $$$r\times c$$$ grid.
• Each cell is either a solid cell, empty cell, or a water cell.
• Initially, all water cells are on the topmost row.
• No solid cell is found on the topmost row.
• While the diagram is modelled as an $$$r\times c$$$ grid, the simulated area itself is still infinite in all four directions. All cells outside the $$$r\times c$$$ grid are initially empty cells.
• You distinguish between two different types of water cells:
  • A water cell is running if there exists an empty cell that can be reached from that water cell by only going left, right, or down, and doesn't pass through solid cells (i.e., only passes through water cells and empty cells).
  • A water cell is still if it is not running.
• Instead of simulating time continuously, you decide that changes only happen at 1 second intervals.
• The only kind of change that can happen is that an empty cell might turn into a water cell. An empty cell turns into a water cell in the next second if and only if at least one of the following is true:
  • It is directly below a water cell. (This represents water falling down.)
  • It is directly above a still water cell. (This represents water overflowing.)
  • It is directly to the left or right of a water cell that's directly above either a solid cell or a still water cell. (This represents water flowing to the side.)

With these rules in place, you now wish to know which cells become water cells, and precisely when they turn into water cells. We denote the cell at row $$$i$$$ (from top to bottom) and column $$$j$$$ (from left to right) by $$$(i, j)$$$. If cell $$$(i, j)$$$ will eventually turn into a water cell, let $$$w(i, j)$$$ be the number of seconds since the beginning when that cell first turns into a water cell. (Note that $$$w(i, j) = 0$$$ for all cells $$$(i, j)$$$ that are initially water cells.) Your goal is to compute $$$w(i, j)$$$ for every cell $$$(i, j)$$$ that will eventually turn into a water cell.

The first line contains $$$t$$$, the number of test cases. The $$$t$$$ test cases follow.

The first line of each test case contains two space-separated integers $$$r$$$ and $$$c$$$ denoting the number of rows and columns of the puzzle grid. Each of the next $$$r$$$ lines contains a string of $$$c$$$ characters indicating a row of the initial grid. Each character is either #, . or W with the following meanings:

• # denotes a solid cell;
• . denotes an empty cell;
• W denotes a water cell.

Constraints

$$$1 \le t \le 10^4$$$

$$$1 \le r, c \le 150000$$$

$$$rc \le 1500000$$$

The sum of the $$$rc$$$ in a single file is $$$\le 1500000$$$.

There is at least one W.

All W's appear in the first row.

No solid cells appear in the first row.

For each test case, first print a single line containing the maximum $$$w(i, j)$$$ among all cells $$$(i, j)$$$ that will eventually turn into a water cell. Then print $$$r$$$ rows, each containing a string of $$$c$$$ characters. The $$$j$$$th character in the $$$i$$$th line is:

• # if cell $$$(i, j)$$$ is a solid cell;
• . if cell $$$(i, j)$$$ is an empty cell that will never turn into a water cell;
• The last digit of $$$w(i, j)$$$ if cell $$$(i, j)$$$ will eventually turn into a water cell.

4
23 49
.......................W.........................
.................................................
....................#....#.......................
....................#....#.......................
....................#....#############...........
..........###########................#...........
..........#..............###########.#...........
..........#.#########....#.........#.#...........
..........#.#.......#....#......#.......#........
..........#.#.......######......#.......#........
........#.....#.................#.......#######..
........#.....#####.........#####.............#..
...######.........#.........#...#.......#####.#..
...#....#.....###.#.........#.###.......#...#.#.#
...#.####.....#.#.#.........#.#.#########.#.#.#.#
...#.#..#######.#.#.........#.#...........#.....#
...#.#..........###......#..#.#.#.........#.....#
#..#.#..#.....#.....#....#......#.........#.....#
#..#.#..#.....#.....#....#......#.........#.....#
#.......#.....#.....#....#......#.........####.##
#.......#.....#.....#....#......#................
#.......#.....#######....########................
#########........................................
23 49
.......................W.........................
.................................................
....................#....#.......................
....................#....#.......................
....................#....#############...........
..........###########................#...........
..........#..............###########.#...........
..........#.#########....#.........#.#...........
..........#.#.......#....#......#.......#........
..........#.#.......######......#.......#........
........#.....#.................#.......#######..
........#.....#####.........#####.............#..
...######.........#.........#...........#####.#..
...#..........###.#.........#.###.......#...#.#.#
...#.####.....#.#.#.........#.#.#########.#.#.#.#
...#.#..#######.#.#.........#.#...........#.....#
...#.#..........#.#......#..#.#.#.........#.....#
#..#.#..#.....#.....#....#......#.........#.....#
#..#.#..#.....#.....#....#......#.........#.....#
#.......#.....#.....#....#......#.........#######
#.......#.....#.....#....#......#................
#.......#.....#######....########................
#########........................................
11 12
...W........
............
..######.#..
..#....#.#..
..#.#..#.#..
..#.#..#.#..
..#.#..#.#..
..#.####.#..
..#......#..
..########..
............
15 20
..W.................
.....############...
.....#..........#...
.....#.########.#...
.....#.#......#.#...
.....#.#............
.....#.#.....#...#..
.....#.#.....#####..
.....#.#............
.....#.#............
.....#.#............
.#...#.#.#..........
.#.......#...#...#..
.#########...#####..
....................

87
.......................0.........................
.......................1.........................
....................#..2.#.......................
....................#..3.#.......................
....................#..4.#############...........
..........###########4454567890123456#...........
..........#21098765432262###########7#...........
..........#3#########1171#.........#8#...........
..........#4#.......#0989#......#...9...#........
.......654#5#456....######......#...0...#........
.......7#33633#78901............#...1...#######..
..321098#22722#####2........#####9992999012345#..
..4######448445678#3........#...#8883888#####6#..
..5#6789#33933###9#4........#.###7654567#...#7#.#
..6#5####21012#.#0#5........#.#.#########.#.#8#.#
..7#4#..#######.#1#6........#.#...........#..9..#
438#3#3345...109###790...#..#.#.#.........#..0..#
#29#2#22#6...2#88888#1...#......#.........#..1..#
#10#1#11#7...3#77779#2...#......#.........#4323.#
#0100000#8...4#66660#3...#......#.........####4##
#9299999#9...5#54321#4...#......#.............5..
#4345678#0...6#######5...########.............6..
#########1...7.......6........................7..
159
.......................0.........................
...................21001012......................
...................3#9929#3......................
...................4#8838#4567890123456..........
.........54321098765#7747#############7..........
.........6###########2252345678901234#8..........
.........7#21098765432262###########5#9..........
.........8#3#########1171#.....9877#6#7789.......
.........9#4#.......#0989#.....0#6667666#0.......
.......432#5#234....######.....1#5558555#1234567.
.......5#11611#56789.......65432#4449444#######8.
..109876#00700#####0.......7#####5550555678901#9.
..2######228223456#1.......8#09876661666#####2#67
..3#8765433933###7#2.......9#1###5432345#765#3#5#
..4#9####21012#.#8#3.......0#2#.#########8#4#4#4#
..5#0#..#######.#9#4....8766#3#678.......9#33533#
544#1#4456...210#0#012..9#55#4#5#9.......0#22622#
#33#2#33#7...3#99199#3..0#444544#0.......1#11711#
#22#3#22#8...4#88288#4..1#333633#1.......2#09890#
#1114111#9...5#77377#5..2#222722#2.......3#######
#0005000#0...6#65456#6..3#109890#3.......4.......
#9876789#1...7#######7..4########4.......5.......
#########2...8.......8..5........5.......6.......
32
...0........
.3212345690.
.4######7#1.
.5#3452#8#2.
.6#2#61#9#3.
.7#1#70#0#4.
.8#0#89#1#5.
.9#9####2#6.
.0#876543#7.
.1########8.
.2........9.
54
..0.................
..1..############...
..2..#8901234567#...
..3..#7########8#...
..4..#6#......#9#...
..5..#5#....5430345.
..6..#4#....6#212#6.
..7..#3#....7#####7.
..8..#2#....8.....8.
..9..#1#....9.....9.
10000#0#012.0.....0.
2#199#9#9#3.1.....1.
3#2345678#4.2#...#2.
4#########5.3#####3.
5.........6.4.....4.

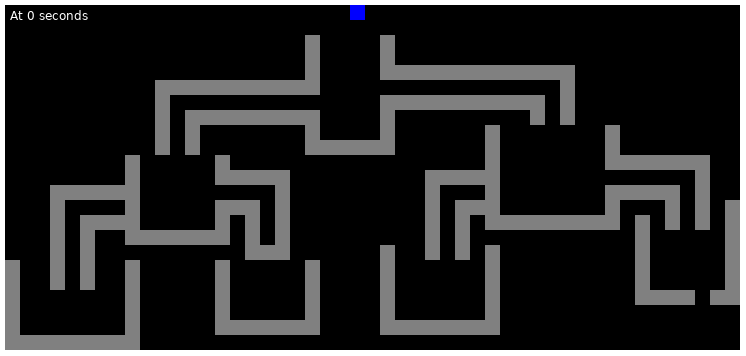
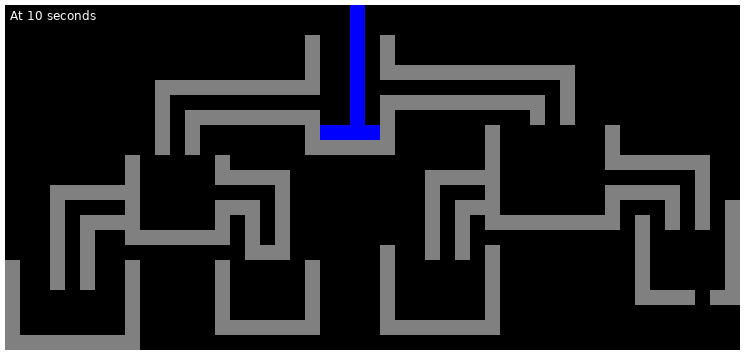
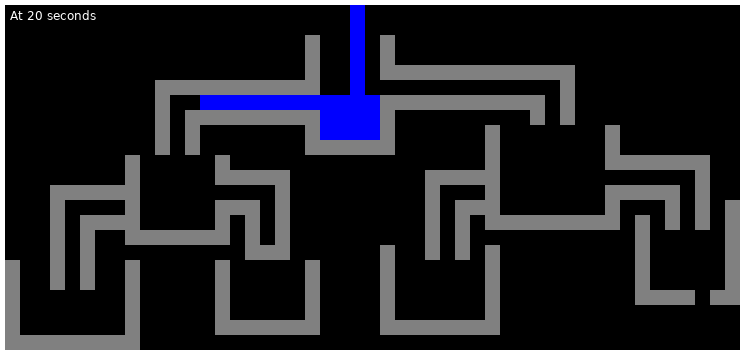
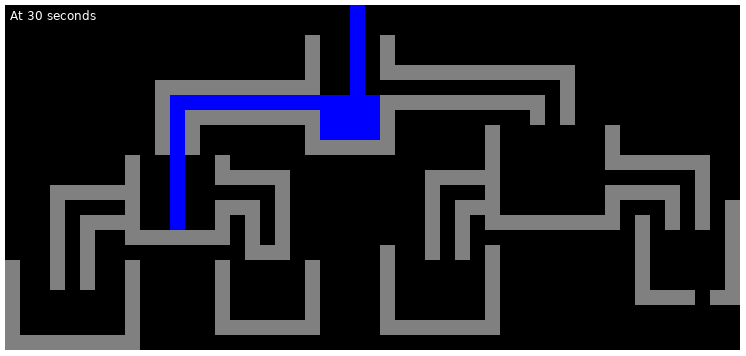
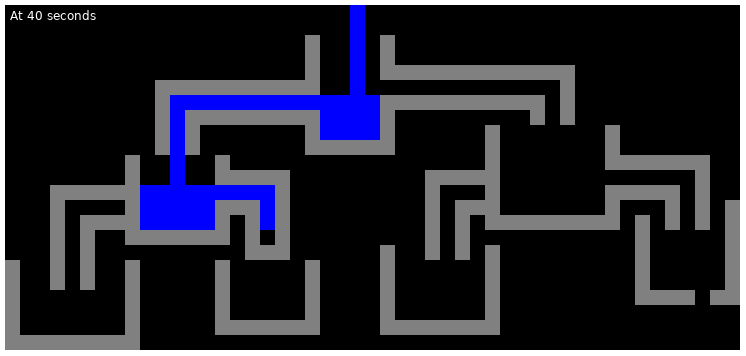
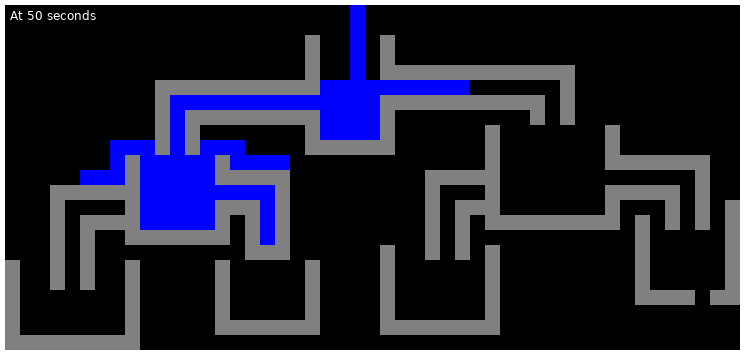
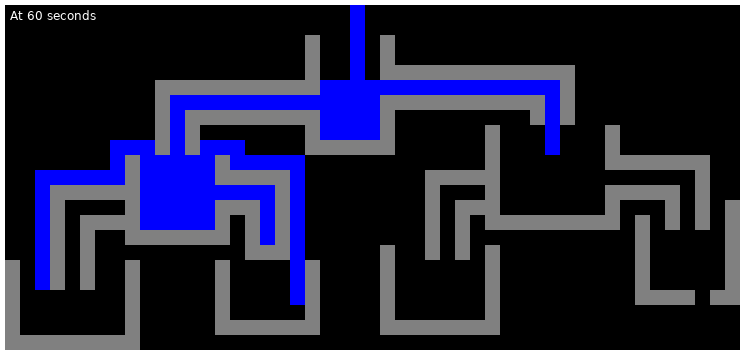
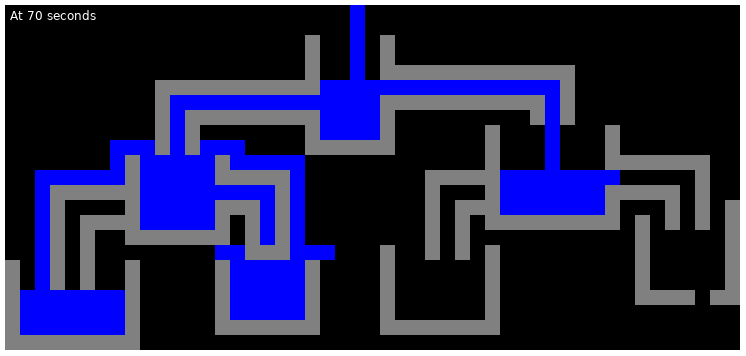
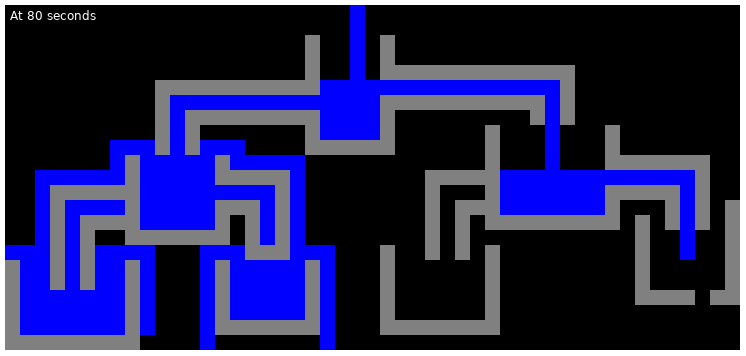
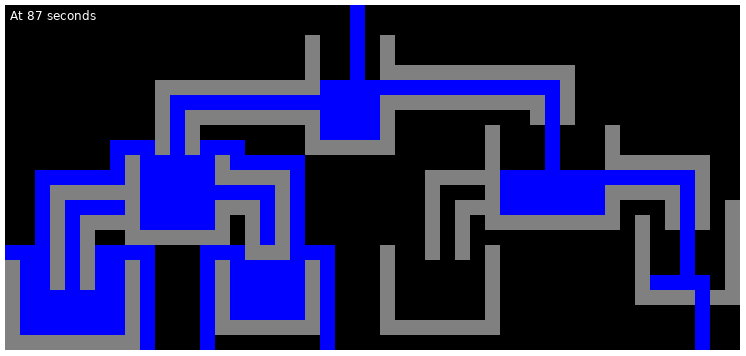
The following are the illustrations of the state of the first test case at various points in time: