406273: GYM102341 L Lati@s

Latias and Latios are usually living together in peace, but recently they started arguing which of them is actually better. In order to resolve this issue, they agreed to play the following game.

The state of the game will contain a multiset of tuples. Each of them will contain exactly $$$n$$$ non-negative integers. In one move a player must choose any of these tuples, as long as it doesn't contain any zero. Let's call this tuple $$$A$$$. The player now performs the following move:

Firstly, choose some other tuple $$$B$$$ (the multiset doesn't have to necessarily contain any copy of $$$B$$$), such that $$$B$$$ also contains $$$n$$$ non-negative integers and each element of $$$B$$$ is strictly smaller than the corresponding element of $$$A$$$; that is, $$$B_i < A_i$$$ for each $$$i = 1, 2, \dots, n$$$. Nextly, a single copy of $$$A$$$ is removed from the multiset. Then, for each non-empty subset $$$X$$$ of integers from $$$1$$$ to $$$n$$$, we add $$$C_X$$$ to the multiset. $$$C_X$$$ is a tuple such that $$$(C_X)_i = B_i$$$ if $$$i \in X$$$, or $$$(C_X)_i = A_i$$$ otherwise. For example, if $$$A=(3, 7)$$$ and $$$B=(0, 2)$$$, then the tuples $$$(0, 7)$$$, $$$(3, 2)$$$ and $$$(0, 2)$$$ will be added to the multiset. Notice that $$$2^n-1$$$ distinct tuples are always added in this step.

The player which is unable to make a move loses.

It wasn't easy for Latias and Latios to decide what multiset should be the starting one. As they happened to have an $$$n \times n$$$ matrix $$$M$$$ consisting of integers, they agreed to create a multiset containing $$$n!$$$ tuples. For each permutation $$$\sigma$$$ of the integers from $$$1$$$ to $$$n$$$, the tuple $$$(M_{1,\sigma(1)}, M_{2,\sigma(2)}, \dots, M_{n,\sigma(n)})$$$ is added to the multiset.

Latias goes first and then the players keep moving alternately. We can prove that the described game is finite, so it's always possible to determine the winner. Your task is to decide who will win assuming that both players play optimally.

The first line contains one integer $$$n$$$ ($$$1 \leq n \leq 150$$$).

Then come $$$n$$$ lines, each consisting of $$$n$$$ integers. The $$$j$$$-th integer in the $$$i$$$-th of these lines equals $$$M_{i, j}$$$ ($$$0 \leq M_{i, j} < 2^{64}$$$).

Please note that the numbers may not fit in the standard $$$64$$$-bit signed type.

Output Latias or First if the first player (Latias) will win the game. Otherwise output Latios or Second. If you decide the winner correctly, both possible words will be accepted.

3
0 1 2
1 2 3
1 2 1

First

2
1 2
2 3

Second

Latias is also a correct answer for the first sample test. Similarly, Latios is a correct answer for the second sample test. Sorry, but Lati@s is never considered correct.

Here is how the game in the second sample test may look:

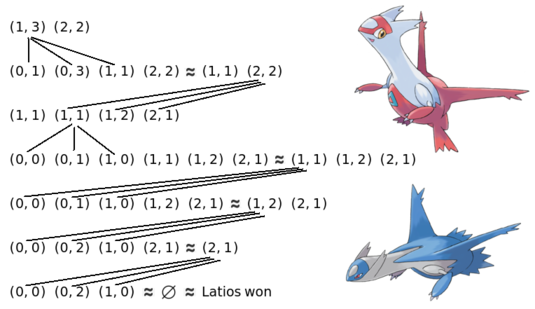
As it's not possible to do any move from a tuple containing any zero, such tuples are omitted. The strategy above is optimal for Latios, i.e. it never gives Latias a chance to win.