406270: GYM102341 I Infernape

Monkeys live on the trees, right? Infernape probably too. There is a tree with $$$n$$$ vertices (a tree is a connected undirected graph without cycles) and $$$q$$$ independent queries. Vertices are numbered with integers from $$$1$$$ to $$$n$$$.

In each query, there are $$$k$$$ Infernape in the vertices of the tree ($$$k$$$ may be different for different queries). The $$$i$$$-th of them sits in the vertex $$$v_i$$$ and has power $$$r_i$$$. Infernape heats all vertices which are in the distance less than or equal to its power from $$$v_i$$$. The distance between two vertices is the number of edges on the shortest path between them. The powers are non-negative, so each Infernape always heats its own vertex. Your task is to answer how many vertices are heated by at least $$$k-1$$$ Infernape.

The first line contains one integer $$$n$$$ ($$$2 \leq n \leq 100\,000$$$) — the number of vertices in the tree.

The $$$i$$$-th of the next $$$n-1$$$ lines describes the $$$i$$$-th edge of the tree and contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$) — the endpoints of this edge.

It's guaranteed that the edges describe a correct tree.

The next line contains one integer $$$q$$$ ($$$1 \leq q$$$) — the number of queries.

Each of the following $$$q$$$ blocks describes one query.

Each block starts with a line with a single integer $$$k$$$ ($$$2 \leq k \leq 300\,000$$$) — the number of Infernape in the current query.

Nextly, each block contains $$$k$$$ lines. The $$$i$$$-th of them contains two integers $$$v_i$$$ and $$$r_i$$$ ($$$1 \leq v_i \leq n$$$, $$$0 \leq r_i \leq n-1$$$) — the index of the vertex at which the $$$i$$$-th Infernape sits and the power of this Infernape.

The sum of $$$k$$$ over all queries in one test doesn't exceed $$$300\,000$$$.

Output $$$q$$$ lines. The $$$i$$$-th of them should contain the number of vertices heated by at least all but one Infernape in the $$$i$$$-th query.

10
1 3
6 4
9 8
1 8
3 4
2 8
10 3
4 5
8 7
2
3
8 1
3 1
3 2
2
7 3
6 0

5
7

Here's how the tree in the sample test looks like:

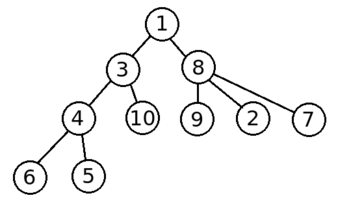
And here is how the queries look like:

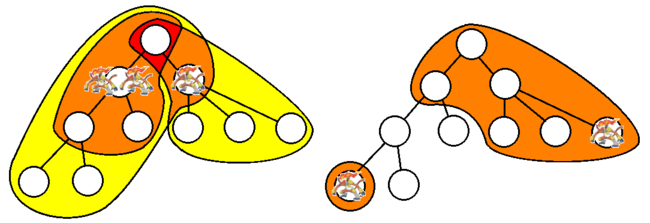
The red area is heated by all Infernape while the orange one is heated by all but one.