406083: GYM102263 E Longest path Problem
Description
You are given a weighted undirected connected tree that contains n nodes and n - 1 edges.
every edge has a weight and there is exactly one path between every pair of different nodes.
Now you should take each edge independently and do the following :
1.remove the edge from tree (that will divide the tree into two components).
2.reconnect the edge again in which it is still a connected tree (every end of the edge should be connected to a node from a different component).
You should do this so that the longest path in the tree is minimised.
InputFirst line contains one integer n (2 ≤ n ≤ 200000)
The next n - 1 lines will contain 3 integers for each,u v w (1 ≤ u, v ≤ n) (1 ≤ w ≤ 109), which means that there is an edge of weight w connecting the nodes u and v.
it is guaranteed that the edges describes one connected tree.
Outputyou should print n - 1 lines, the ith line should be the answer for the ith edge.
ExampleInput4Output
1 2 2
1 3 3
2 4 2
7Note
5
5
The sample graph 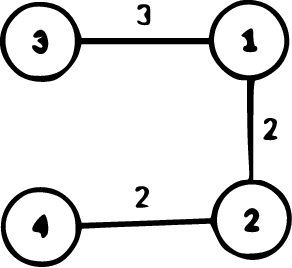
Solution for the second edge: after removing the second edge, add it to again between Node 2 and Node 3