406010: GYM102218 C Circuit Unstable

While in his circuits class, Oscar was asked to build the following circuit:

That is:

• We have a DC (Direct Current) voltage source of $$$V$$$ Volts that feeds the whole circuit.
• There is a capacitor of capacitance $$$C$$$ Farads and an inductor of inductance $$$L$$$ Henrys, both connected in parallel.
• We have a resistor of resistance $$$R$$$ Ohms connected in series with the previous block.
• The initial current of the inductor and the initial voltage of the capacitor are both zero.

And then he was asked to measure the voltage $$$V_r(t)$$$ in the resistor, by varing all the parameters. To accomplish that, he will use the oscilloscope available in the electronic lab to graph the value of $$$V_r(t)$$$ with respect to time (in seconds). He noticed some amazing pattern: $$$V_r(t)$$$ tends to stabilize at the value of the voltage input $$$V$$$ after some few seconds of oscillation, no matter what are the values of $$$R,L,C$$$ (but they must satisfy $$$L < 4R^2 C$$$), as shown in the graph below (the graph corresponds to the sample test case):

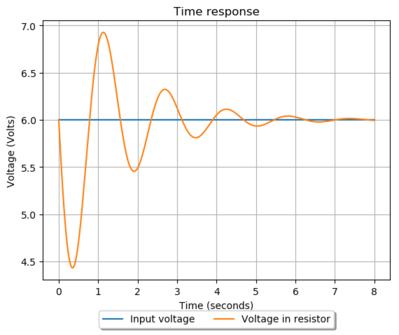
Oscar doesn't like at all that this behaviour tends to overshot and undershot the voltage $$$V_r(t)$$$ because that's bad in many daily-life applications (for example, in analog filters it can damage all the electronic elements due to the excesive voltage). He also doesn't have many resistors, inductors nor capacitors in his toolbox to experiment, so he asks you to find the minimum and maximum values for $$$V_r(t)$$$ and the time at which they ocurr before it stabilizes, without having to build physically the circuit.

In the only line of input there are four space-separated real numbers: $$$V$$$, $$$R$$$, $$$L$$$ and $$$C$$$, the parameters of the circuit described above. It is guaranteed that $$$1 \leq V \leq 20$$$, $$$0.1 \leq R, L, C \leq 20$$$ and $$$L < 4R^2 C$$$.

Print two lines of output, each with two real numbers:

• In the first line: the time in seconds at which the minimum value occurs and then the minimum value itself in Volts.
• In the second line: the time in seconds at which the maximum value occurs and then the maximum value itself in Volts.

The absolute or relative error of the answers should not exceed $$$10^{-6}$$$.

6 3.7 0.3 0.2

0.348848049 4.430980248
1.129139119 6.926100394

Here is a quick remainder about how circuits work:

1. The current flowing into a node must be the same as current flowing out of that node. For example, in the above circuit, we have $$$I_r(t)=I_l(t)+I_c(t)$$$.

2. Around a closed loop, the sum of the voltage rises must be equal to the sum of the voltage drops. For example, in the above circuit, we have $$$V = V_r(t) + V_l(t)$$$ and $$$V_c(t) = V_l(t)$$$.

3. The governing law of the three elements presented in the above circuit is:
   • For resistor with resistance $$$R$$$ Ohms, we have $$$V_r(t)=RI_r(t)$$$.
   • For an inductor with inductance $$$L$$$ Henrys, we have $$$V_l(t)=L\frac{d}{dt}I_l(t)$$$.
   • For a capacitor with capacitance $$$C$$$ Farads, we have $$$I_c(t)=C\frac{d}{dt}V_c(t)$$$.