405704: GYM102051 E Nate and Enigmatic Torches

E. Nate and Enigmatic Torchestime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Nate has $$$3$$$ special types of torches, with colors red, blue, and yellow that combines colors subtractively and not additively. The colors mentioned, as Nate had learned in grade school, are the primary colors. When the light from the primary torches overlap, they have the following behavior:

• When red light overlaps with blue light, it produces violet.
• When blue light overlaps with yellow light, it produces green.
• When red light overlaps with yellow light, it produces orange.

Violet, green, and orange are considered "secondary colors."

When an area is affected by two torches of the same color, the color is amplified in that area. Let's call the number of torches that give the same color to an area as the power. Light becomes secondary color if and only if the two colors that affect the area are of the same power.

Now, when things get more complicated than the secondary colors, the lights get confused. Normally, when we mix violet paint with red paint, we get the color red-violet. But this is not so for the light from Nate's torches. Let's put another torch in an area affected by one of the secondary colors. If that torch is one of the component colors of the secondary color in the area, the mixed light becomes pink. But when the torch is not one of the component colors, the mixed light becomes brown.

Nate places $$$k$$$ of these torches in a field of $$$m \times n$$$ grid. Each tile of the grid is labeled with coordinate $$$(x, y)$$$, from the upper-left hand corner, whose coordinate is $$$(1, 1)$$$. Each torch has a color, denoted by RED, BLUE, and YELLOW.

When placed in a field, the torch lights up a square area of side length $$$s$$$ with the torch being in the center of that square. Let us call the side length the range. The location of the $$$i$$$th of the $$$k$$$ torches, with color $$$c_i$$$, is denoted by $$$(x_i, y_i)$$$. If the range of the torch is odd, then $$$(x_i, y_i)$$$ corresponds to the center tile of the square area lit up by the torch. If the range of the torch is even, then $$$(x_i, y_i)$$$ corresponds to the upper-left tile of the four center tiles of the square area lit up by the torch. The torch itself is placed in the middle of the four center tiles. Refer to the diagram below for a visualization. It is guaranteed that no two torches are placed in the exact same location, because that would be violating Pauli's Exclusion Principle. Nate wants to find out how many tiles inside the $$$m \times n$$$ grid are lit up with the color $$$c$$$.

Input

The first line of input contains three space-separated integers $$$m$$$, $$$n$$$, and $$$k$$$, respectively. The first integer, $$$m$$$, is the horizontal length of the grid. The second integer, $$$n$$$, is the vertical length of the grid. The third integer, $$$k$$$, is the number of torches Nate will place. The next line of input contains $$$c$$$, the color that Nate wants. It is guaranteed that $$$c$$$ is one of the following: RED, BLUE, YELLOW, GREEN, ORANGE, VIOLET, BROWN, PINK. Each of the next $$$k$$$ lines of input contains four space-separated integers $$$c_i$$$, $$$x_i$$$, $$$y_i$$$, and $$$s$$$, respectively. The first integer, $$$c_i$$$, is the color of the torch placed. The second integer, $$$x_i$$$, is the $$$x$$$-coordinate of the center tile. The third integer, $$$y_i$$$, is the $$$y$$$-coordinate of the center tile. The fourth integer, $$$s$$$, is the side length of the square region that the torch lights up. It is guaranteed that $$$c_i$$$ is one of RED, BLUE, and YELLOW.

Constraints

$$$1 < m, n \leq 50 $$$

$$$1 \leq k \leq m \times n$$$

$$$1 \leq x_i \leq m$$$

$$$1 \leq y_i \leq n$$$

$$$1 \leq s \leq 50$$$

Output

Output a single integer, the number of tiles that are lit up as the color $$$c$$$.

ExamplesInput

2 2 1
RED
RED 1 1 1

Output

1

Input

2 2 2
BLUE
RED 1 1 2
BLUE 1 1 1

Output

0

Input

2 2 1
RED
RED 2 2 2

Output

1

Note

In the first test case, the red torch has a range of $$$1$$$. It is placed in the middle of the $$$(1, 1)$$$ tile.

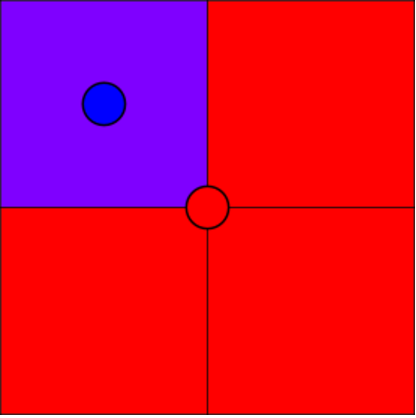
In the second test case, the red torch has a range of $$$2$$$. The upper-left tile of the four center tiles is $$$(1, 1)$$$. The red torch is placed accordingly. The blue torch has a range of $$$1$$$, placed in the middle of the $$$(1, 1)$$$ tile. The red and the blue in the $$$(1, 1)$$$ tile overlaps, making the $$$(1, 1)$$$ tile color violet.

In the third test case, the red torch has a range of $$$2$$$. The upper-left tile of the four center tiles is $$$(2, 2)$$$. The red torch is placed on the corner of the field. Since we are only interested in the number of tiles lit with red light within the $$$2 \times 2$$$ field, the answer is $$$1$$$.