405599: GYM102006 L Sad Meals

Based on a sad story.

Mr. Light is living abroad and unfortunately, he doesn't know how to cook much meals. The day he learns how to cook a new meal, he will cook that meal for that day. Starting from the next day and assuming he now knows how to cook x meals, he will then start circulating between them, cooking one meal per day in the order he learned them in; from 1 to x then back to 1 again, until he learns a new meal. On day 1, Mr. Light learns how to cook the first meal.

For example, here is a valid sequence of meals he ate during the span of his first 15 days, assuming he learned to cook a new meal on days 1, 3, 7, and 9:

Here is an invalid sequence, since he never learned how to cook his third meal:

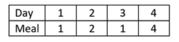
Note that it is possible for Mr. Light to learn new meals in consecutive days (check the second sample test).

You will be given the meals he cooked on his first n days, except that some of them will be missing. Can you figure out the minimum number of meals he could have learned in those n days? Also output a valid sequence with the missing numbers filled with a valid meal he could have cooked that day.

The first line of input contains a single integer T (1 ≤ T ≤ 4096), the number of test cases.

The first line of each test case contains a single integer n (2 ≤ n ≤ 10⁵), the number of days.

The next line contains n space-separated integers v₁, v₂, ..., v_n (0 ≤ v_i ≤ n), where v_i is equal to the meal number he ate on the i^th day if v_i > 0. Otherwise if v_i = 0, the meal number is missing on that day. It is guaranteed that v₁ = 1, and there's at least one missing number.

It is guaranteed that for each test case, there is at least one way to fill the missing numbers to make a valid sequence.

The sum of n over all test cases doesn't exceed 6 × 10⁶.

For each test case, output the minimum number of meals k Mr. Light could have learned, on the first line.

One the second line, output n space-separated integers d₁, d₂, ..., d_n (1 ≤ d_i ≤ k), where d_i is a valid meal he could have cooked on the i^th day. The non-zero numbers from input must not change.

If there's more than one valid way to fill the missing meals, print any of them.

2
4
1 1 0 3
9
1 0 1 0 0 0 2 0 5

3
1 1 2 3
5
1 2 1 3 4 1 2 3 5