405038: GYM101745 C Infinite Graph Game

Eugene has an undirected graph with n nodes and m edges. The nodes are labeled from 1 to n. The i-th node initially has value v_i. Eugene also has some sequence of nodes s₁, s₂, ..., s_k. Nodes can appear in this sequence in arbitrary order, two neighboring elements of the sequence are not necessary neighboring nodes of the graph. Moreover, two neighboring elements can stand for the same node. Each node can appear in this sequence arbitrary (possibly zero) number of times.

Eugene plays the following game starting at second 0 infinitely:

1. On the i-th second, he chooses node .
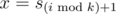2. Adds to his score the value of all neighbors of x.
3. Divide the value v_x by 2. Note that we consider standard division, not integer. Thus, real value v_x can turn to be non-integer.

Let l_i be Eugene's score after the i-th second. If sequence l_i grows infinitely large, print -1.

Otherwise, as sequence l_i is non-decreasing and doesn't go infinitely large, it has a limit. Moreover, one can show that this limit a rational number and can be represented as 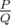, where P and Q are coprime integers.

Under the given constraints, it is guaranteed that Q is not divisible by 10⁹ + 7.

Print the value of P·Q^- 1 modulo 10⁹ + 7.

Here Q^- 1 denotes the multiplicative inverse of Q modulo 10⁹ + 7.

The first line of the input contains three integers n, m and k (1 ≤ n, m, k ≤ 100 000) — the number of nodes in the graph, the number of edges and the length of sequence s.

The next line of the input contains n integers, v₁, v₂, ..., v_n (0 ≤ v_i ≤ 10⁹) — initial values of each node.

The next line of input contains k integers, s₁, s₂, ..., s_k (1 ≤ s_i ≤ n) — the sequence Eugene uses to consider nodes.

Each of the next m lines of the input contains two integers u_i and v_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i), that denote an undirected edge between corresponding nodes. It is guaranteed that each pair of nodes is connected by no more than one edge.

Print a single integer, the answer to the problem.

4 3 4
1 1 1 1
1 2 3 4
1 2
2 3
1 3

9

For the sample, Eugene will choose nodes 1, 2, 3, 4, 1, 2, 3, 4, ...

The first few steps looks as follows:

1. Choose node 1. Its value becomes . We add 2 to his score.
2. Choose node 2. Its value becomes . We add to his score.
3. Choose node 3. Its value becomes . We add 1 to his score.
4. Choose node 4. Value v₄ becomes . We add 0 to his score.

If we continue this infinitely, we can show that the limit of his score is equal to 9.