405009: GYM101736 I LASER SHIELDs

Our green Cactus friend is in danger again! A hostile troop of cacti is trying to attack this lonely cactus. Luckily, Cactus happens to have N LASER SHIELDs. However, Cactus can only activate up to k LASER SHIELDs, and he wants you to help him determine the best way to use k LASER SHIELDs.

Each LASER SHIELD has an activation time t_i at which it can be activated. If it is not activated at that time, it loses its power and becomes useless forever. Each LASER SHIELD has an initial power p_i and a corrosion rate r_i. When a LASER SHIELD is activated, it will have the initial power p_i and lose power at the rate of r_i power units per second. When the power of a LASER SHIELD drops below 0, it becomes inactive and cannot be used again.

Define the defense power at a specific time to be the maximum power over all activated shields. The defense power is 0 if there are no active shields. Define the protection of Cactus to be the minimum defense power at any time during the attack.

Cactus used w3m to look into the future, seeing that the hostile cacti begin their attack at time t_s and end their attac at time t_e. Your task is to determine the maximum possible protection of Cactus.

The first line contains a two space-separated integers n and k (0 ≤ n, k ≤ 10⁵), the total number of LASER SHIELDs and the number of LASER SHIELDs that Cactus can activate respectively.

Each of the next n lines contains three space-separated integers t_i, p_i, and r_i (0 ≤ t_i ≤ 10⁹;1 ≤ p_i, r_i ≤ 10⁹), describing the ith LASER SHIELD.

The last line of input contains two space-separated integers t_s and t_e (0 ≤ t_s < t_e ≤ 10⁹), the start and end times of the attack respectively.

Print, on a single line, the maximum possible 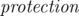that can be achieved.

4 3
2 10 4
3 6 1
7 3 1
8 12 1
4 9

2

In the first sample, it is optimal to activate the second, third, and fourth shields.