404646: GYM101597 I The Secret

The random integer y is either zero or one, and the random integer x is between 1 and N. The value y is a secret. We are given an interval , and we need 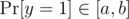to hold at all times in order to guarantee the confidentiality of the secret. (I.e. we want that .)

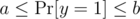The values and are known for all i between 1 and N. Unfortunately, the dependency between x and y means that someone who learns x might be able to compute good bounds on 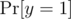. Fortunately, the value of x is not yet known. Your goal is to censor the value of x such that nobody can learn too much about the value of y.

To censor x means to partition the set {1, 2, ..., N} into equivalence classes A₁, ..., A_M such that, as soon as x is determined, only the index i of the unique equivalence class A_i that contains x becomes known (instead of the precise value of x).

You therefore have to find a partition such that for all i between 1 and M, the confidentiality of the secret is maintained, i.e. .

(Hint: Recall that 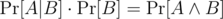, where means that both A and B are true, and .)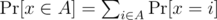

In case there are multiple solutions, compute an arbitrary solution that maximizes the number of equivalence classes that contain only a single element.

The first line of the input contains two space-separated integers A and B such that a·10⁶ = A and b·10⁶ = B. The second line of the input contains the single integer N (1 ≤ N ≤ 10⁶).

The i-th of the next N lines of the input contains integers X_i and Y_i such that and .

If there is no solution, print the single integer  - 1.

Otherwise, the first line of the output should contain the size M of the partition. The i-th of the following M lines should contain an integer K_i, the number of elements of the i-th equivalence class A_i, followed by K_i numbers, the elements of A_i.

You may print the equivalence classes and their elements in any order.

450000 550000
6
100000 449999
100000 550001
100000 400000
100000 600000
300000 500000
300000 500000

4
2 1 2
2 3 4
1 5
1 6

500000 500000
5
200000 500000
200000 500000
200000 500000
200000 500000
200000 500000

5
1 1
1 2
1 3
1 4
1 5

228503 520839
1
1000000 379204

1
1 1