404515: GYM101522 G Gravitational Tetris

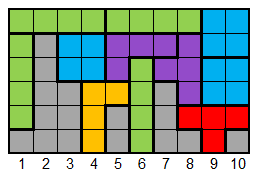
Gravitational Tetris is a Tetris variant that individual blocks can freely fall to the bottom. Therefore the game state of Gravitational Tetris can be described by an array of 10 integers, each representing the number of blocks (the height) of the column. The columns are numbered from 1 to 10. For example, the game state below can be described by the array [1, 5, 3, 0, 2, 0, 3, 1, 0, 1].

You are given a valid Gravitation Tetris game state. Your task is to continue to play the game such that all blocks are eliminated. A row will be eliminated when there are 10 blocks in the row.

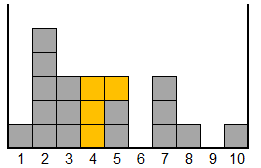
Since the blocks can freely fall, there are only 8 distinct Tetrominoes (shapes), with all rotations taken into account. The letter below each Tetromino denotes its type and its left-most column. In each move, you should select a Tetromino type and a column number c. For type A, it will fall onto column c. For type B, it will fall onto columns c, c + 1, c + 2 and c + 3. For type C, E and G, it will fall onto columns c and c + 1. For type D, F and H, it will fall onto columns c, c + 1 and c + 2. For example, from the above game state, after choosing type G and column 4, it will become:

You are allowed to use at most 1000 moves and there is no height restriction. Completed rows will be eliminated automatically.

The input consists of 10 integers, H₁, H₂, ..., H₁₀ – the height of the columns from left to right. It is guaranteed that it is a valid game state and a solution exists.

0 ≤ H_i ≤ 12. At least one of them is 0 but their sum is not 0.

Output any sequence of moves that can eliminate all blocks. You are not required to minimize the number of moves.

In the first line output a single integer M – the number of moves.

In each of the next M lines output the type of Tetromino (A to H), a space, then the column number (1 to 10). Your answer will be regarded as incorrect if the column number is invalid for the type (e.g. column 8, 9 or 10 for type B).

1 1 0 1 1 1 0 1 0 2

3
B 4
H 1
H 7

1 5 3 0 2 0 3 1 0 1

11
G 4
A 1
A 6
D 8
C 3
C 9
C 9
E 7
F 5
B 1
B 5

Explanation for Sample 1: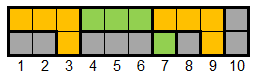

Explanation for Sample 2: