403855: GYM101341 J Catch the Monster

Manse and Eckels are special agents of time patrol. Now they are trying to catch Faceless Chrono Monster, whose existence threatens the integrity of space-time continuum. The monster dwells between worlds on the Time Tree, consisting of n time nodes, connected with time corridors. Each character can move from one node to another through time corridors. There are 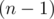time corridors, and any time node can be reached from any other one by moving through the time corridors.

Manse and Eckels can initially appear in two arbitrary (not necessarily distinct) time nodes, wherever they want, after which they would be able to move between time nodes through time corridors independently of each other. As soon as one of them meets the Monster, the Monster will be instantly destroyed, no matter whether it happened in the node or in one of the corridors.

The problem is that the Faceless Chrono Monster moves along the Time Tree many times faster than patrolmen, and, most importantly, foresees the future. Thereby, he knows in advance, in which time nodes the heroes will appear and how they will move, so he can use this, planning his escape. The Monster is unbelievably clever, so he will use his abilities optimally to survive. Will Mance and Eckels be able to destroy the Monster?

The first line contains a single integer n (1 ≤ n ≤ 200000) — the number of time nodes.

The next 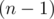lines describe time corridors. They contain two integers each, x_i and y_i, separated by a space (1 ≤ x_i, y_i ≤ n, x_i ≠ y_i) — numbers of time nodes connected by i-th time corridor.

If the heroes will be able to destroy the Monster, output «YES» (without quotes), otherwise output «NO» (without quotes).

4
1 4
2 4
3 4

YES

7
1 2
1 3
2 4
2 5
3 6
3 7

YES

21
1 2
1 3
1 4
1 5
2 6
2 7
2 8
2 9
3 10
3 11
3 12
3 13
4 14
4 15
4 16
4 17
5 18
5 19
5 20
5 21

NO