403765: GYM101262 E Vera and Love Triangles
Description
Vera has N friends numbered from 0 to N - 1. Being in Software Engineering, all her friends do not have enough spare time to engage in relationships. However, friends have crushes on each other.
Let g(x), where x are non-negative integers, be the number of ones in the binary representation of x.
Let f(i, j) = g((A·B(i·N + j))%M), where A, B, M are integer constants.
It is known that for any 2 friends i < j, if f(i, j) is even then i has a crush on j, otherwise j has a crush on i.
Vera thinks love triangles are very funny. A love triangle is a set of 3 friends i, j, k such that i has a crush on j, j has a crush on k and k has a crush on i.
Given integers N, M, A, B tell Vera how many love triangles exist among her friends. Two love triangles are different if they contain a different set of 3 friends.
Constraints:
3 ≤ N, M ≤ 200, 000
0 < A, B < M
N, M, A, B are integers
M is prime
InputThe input will be in the format:
N M A B
OutputOutput one line with the number of love triangles.
ExamplesInput3 5 3 4Output
1Input
3 3 1 2Output
0Input
1337 10007 1337 1337Output
99141170Note
Let 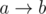 denote that friend a has a crush on friend b.
denote that friend a has a crush on friend b.
For the first example, f(0, 1) = 1, f(0, 2) = 2, and f(1, 2) = 1. So 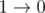 ,
,  , and
, and  , so there is one love triangle.
, so there is one love triangle.
For the second example, 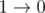 ,
,  , and
, and  , so there are zero love triangles.
, so there are zero love triangles.