403121: GYM101020 E Napoléon

In the world of chess, there is a good plan to start your game with which is “Napoléon plan”. “Napoléon plan” is commonly based on two pieces, (the queen and a bishop), using these two pieces you can guarantee the win after some moves if you are facing a beginner opponent or any way you can start your game with it to explore your opponent qualifications. Further, this plan can be used and applied in proceeding states of your game so you can disperse your opponent before you surprise him/her with a successful apply of “Napoléon plan” and saying your mortal word “checkmate”.

The plan; substantially, says that you can checkmate your opponent king by constricting it with its allies, threatening it with your queen which is guarded; commonly, by your bishop.

The picture displays a successful apply of “Napoléon plan”.

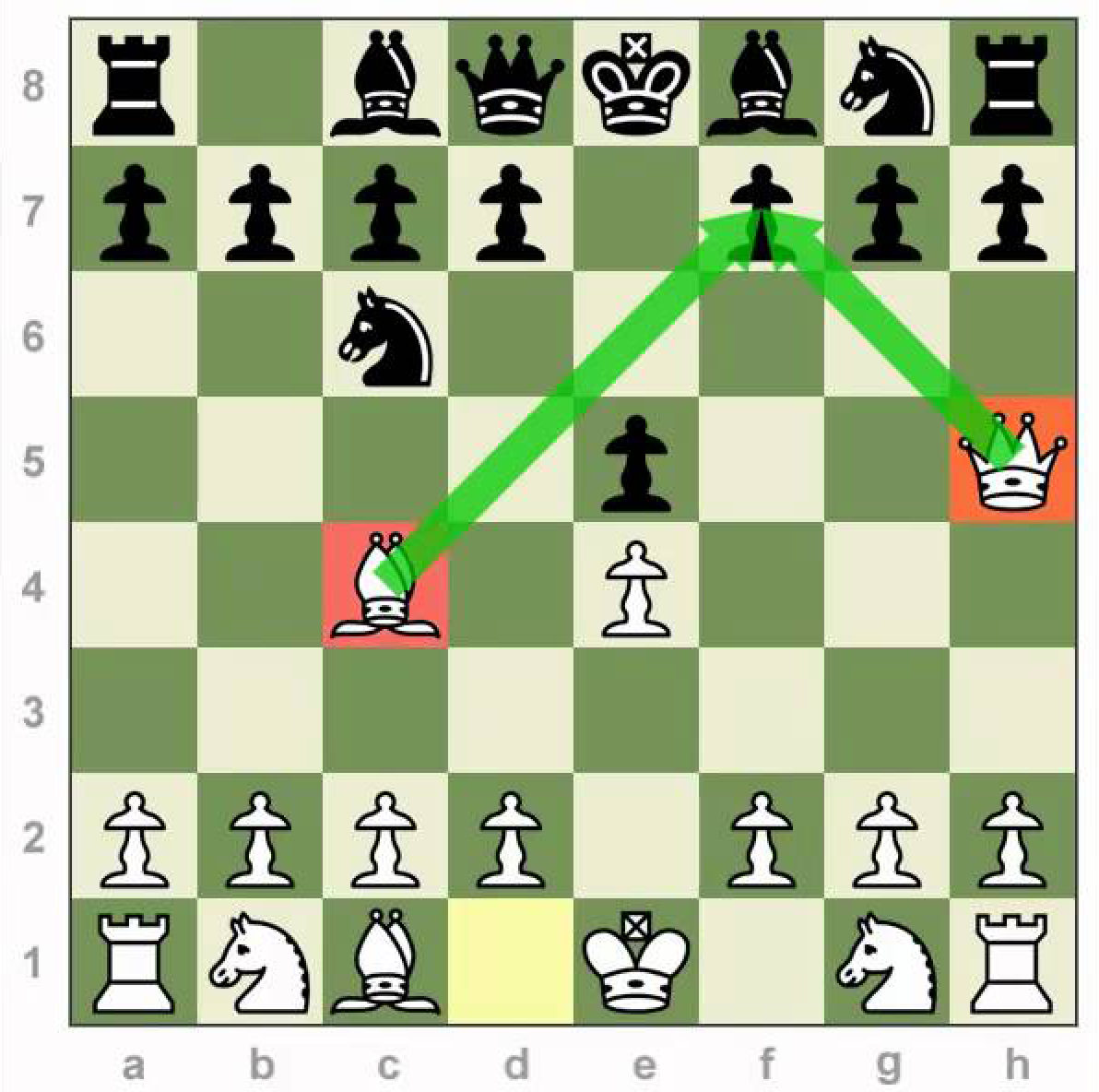
Our problem goes in a further state of the game, when you need to get your bishop to the right state guarding your queen for a successful apply of the plan. Given the Current location of the bishop and its Target state in the form Xc, Yc, Xt, Yt starting the count from zero, tell the queen: the minimum number of squares that the bishop pass in the minimum moves assuming an empty chess board.

The first line of input is the number of test cases 0<T<5000, the second line is an integer for the chessboard size 0<N<=20, then (2*T) lines follow. Each test case is two lines; the first line contains two integers 0<=Xc,Yc<N representing the current location of the bishop, the second line contains another two integers 0<=Xt,Yt<N representing the target location of the bishop.

For each test case, print a line containing the minimum number of squares passed by the bishop on its way to the target location taking the minimal possible moves or print “can't reach!” in case of impossible to reach the target from the current location.

3
8
0 0
7 1
5 5
5 5
0 5
6 7

7
0
6