402491: GYM100792 E Entertainment

The Berland King is hosting a fencing tournament once again. A total of 2^k best fighters from all over the country came to the capital of Berland to compete for the glory and — of course — for formidable cash prizes.

Every fighter is given a number from 1 to 2^k according to his mastery: the strongest fighter is labeled 1, the second strongest fighter is labeled 2 and so on to the weakest fighter, who is labeled 2^k. A standard play-off scheme is implemented: the players are randomly put in the leaves of the tournament bracket which is a full binary tree with 2^k leaves. All initial dispositions are equiprobable. Then the matches are played between all pairs of players sharing a parent in the tournament bracket, with winners advancing to the next stage and losers being eliminated from the tournament. This process continues until there is only one player remaining. It's easy to see that the participants and the results of all games are determined by the initial disposition.

Actually, there is no intrigue: the fighter with the lower number always beats the fighter with the higher number. Still, the matches are entertaining, and some fighters are more fun to watch than the others. More precisely, i-th fighter has an amusement level of a_i; note that some fighters may not be among the strongest, but tend to play amusing matches nonetheless, meaning that a_i doesn't depend from i in any way. If the players with numbers i and j play a match, it has spectacularity equal to a_i·a_j. The entertainment of the whole tournament is defined as the sum of spectacularity of all matches to play.

The number of tickets sold for the matches (and thus, the amount of money made) heavily relies on the spectacularity of the matches. The seeding is not announced yet, and the King requested you to calculate the expectation of tournament's entertainment. Note that the value depends only on the random seeding as all the matches' outcomes are predetermined.

The first line contains the only integer k (1 ≤ k ≤ 18) — the number of tournament rounds.

The next line contains 2^k space-separated numbers a₁, ..., a_2^k (0 ≤ a_i ≤ 10⁹) — amusement levels of the fighters.

Let the expectation of total spectacularity of all matches be equal to the irreducible fraction P / Q. Print the value of P·Q^- 1 in the prime field of integers modulo 1 000 000 007 (10⁹ + 7). It is guaranteed that this modulo does not divide Q, thus the number to be printed is well-defined.

1
2 3

6

2
1 2 3 4

14

2
4 3 2 1

333333358

In the third sample the expectation is 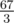.