402231: GYM100705 A1 Rasta-lover Pair

A pair (p, q) of integer numbers is called Rasta - lover if and only if 1 ≤ p, q < n and there is a positive integer like x such that:

p^x ≡ q (modn)

Subtasks 1 - 3:

Given n, calculate the number of Rasta - lover pairs modulo 10⁹ + 7.

Subtasks 4 - 6:

A positive integer p is called n - Rastaly if and only if p < n and there is a positive integer like x such that p^x ≡ 1 (modn) and p and n are coprimes.

For a positive integer n, f(n) is the smallest positive integer a such that for each n - Rastaly number like p, p^a ≡ 1 (modn) (this number always exists).

If M is equal to 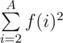for a given A, then you have to calculate M modulo 10⁹ + 7.

Subtasks:

• Subtask A1: n = 1234
• Subtask A2: n = 1111151
• Subtask A3: n = 1234567
• Subtask A4: A = 1234
• Subtask A5: A = 12345
• Subtask A6: A = 1234567

Each subtask consists of one testcase.

Input consists of one number. For subtasks 1-3, it's n and for subtasks 4-6 it's A.

Print the answer modulo 10⁹ + 7 in one line.