401455: GYM100460 A Golden Dragons
Description
Golden dragons are immortal majestic creatures inhabiting Enia since the beginning of times. There are total of n golden dragons in Enia, each one in its own nest. The problem is that some pairs of dragons dislike each other, whereas some pairs of nests are so close to each other that if one roars in one of the nests, it will be clearly heard in another one. Each dragon has at most a enemies, and each nest has at most b neighbour nests. It is also known that n ≥ 3ab.
The dragons are annoyed at the roar of their enemies, so they want to resettle so that each dragon would occupy exactly one nest, and no two enemy dragons would live in neighbour nests.
InputThe first line contains the single integer n (1 ≤ n ≤ 5000) — the number of dragons.
The second line contains the single integer m (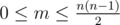 ) — the number of pairs of enemy dragons. Each of the next m lines contains two integers separated by the space: xj and yj (1 ≤ xj < yj ≤ n) — the pair of numbers of two enemy dragons. Each pair occurs only once.
) — the number of pairs of enemy dragons. Each of the next m lines contains two integers separated by the space: xj and yj (1 ≤ xj < yj ≤ n) — the pair of numbers of two enemy dragons. Each pair occurs only once.
The next line contains the single integer k (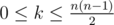 ) — the number of pairs of neighbour nests. Each of the next k lines contains two integers separated by the space: pj and qj (1 ≤ pj < qj ≤ n) — the pair of numbers of two neighbour nests. Each pair occurs only once.
) — the number of pairs of neighbour nests. Each of the next k lines contains two integers separated by the space: pj and qj (1 ≤ pj < qj ≤ n) — the pair of numbers of two neighbour nests. Each pair occurs only once.
In the first line output «Solution exists» (without quotes) if there exists a variant of resettling dragons satisfying the problem's condition. Otherwise output «Wrong answer» (without quotes).
In the first case in the second line output n integers di separated by the spaces, where di is the number of the dragon which should be settled in the i-th nest. If there are multiple answers, output any of them.
ExamplesInput3Output
1
1 2
1
1 3
Solution existsInput
2 1 3
4Output
2
1 2
3 4
2
1 3
2 4
Solution exists
1 2 3 4