311156: CF1942D. Learning to Paint
Description
Elsie is learning how to paint. She has a canvas of $n$ cells numbered from $1$ to $n$ and can paint any (potentially empty) subset of cells.

Elsie has a 2D array $a$ which she will use to evaluate paintings. Let the maximal contiguous intervals of painted cells in a painting be $[l_1,r_1],[l_2,r_2],\ldots,[l_x,r_x]$. The beauty of the painting is the sum of $a_{l_i,r_i}$ over all $1 \le i \le x$. In the image above, the maximal contiguous intervals of painted cells are $[2,4],[6,6],[8,9]$ and the beauty of the painting is $a_{2,4}+a_{6,6}+a_{8,9}$.
There are $2^n$ ways to paint the strip. Help Elsie find the $k$ largest possible values of the beauty of a painting she can obtain, among all these ways. Note that these $k$ values do not necessarily have to be distinct. It is guaranteed that there are at least $k$ different ways to paint the canvas.
InputThe first line contains a single integer $t$ ($1 \leq t \leq 10^3$) — the number of test cases.
The first line of each test case contains $2$ integers $n$ and $k$ ($1 \leq n \leq 10^3$, $1 \leq k \leq \min(2^n, 5 \cdot 10^3)$) — the number of cells and the number of largest values of the beauty of a painting you must find.
The next $n$ lines of each test case describe $a$ where the $i$-th of which contains $n-i+1$ integers $a_{i,i},a_{i,i+1},\ldots,a_{i,n}$ ($-10^6 \leq a_{i,j} \leq 10^6$).
It is guaranteed the sum of $n$ over all test cases does not exceed $10^3$ and the sum of $k$ over all test cases does not exceed $5 \cdot 10^3$.
OutputFor each test case, output $k$ integers in one line: the $i$-th of them must represent the $i$-th largest value of the beauty of a painting Elsie can obtain.
ExampleInput4 1 2 -5 2 4 2 -3 -1 3 8 2 4 3 1 3 5 6 20 0 -6 -3 0 -6 -2 -7 -5 -2 -3 -4 7 0 -9 -4 2 -1 1 1 -2 -6Output
0 -5 2 0 -1 -3 7 5 4 3 3 2 1 0 8 8 7 7 5 5 2 2 1 1 1 1 1 1 0 0 0 0 0 -1Note
In the first test case, Elsie can either paint the only cell or not paint it. If she paints the only cell, the beauty of the painting is $-5$. If she chooses not to paint it, the beauty of the painting is $0$. Thus, the largest beauty she can obtain is $0$ and the second largest beauty she can obtain is $-5$.
Below is an illustration of the third test case.
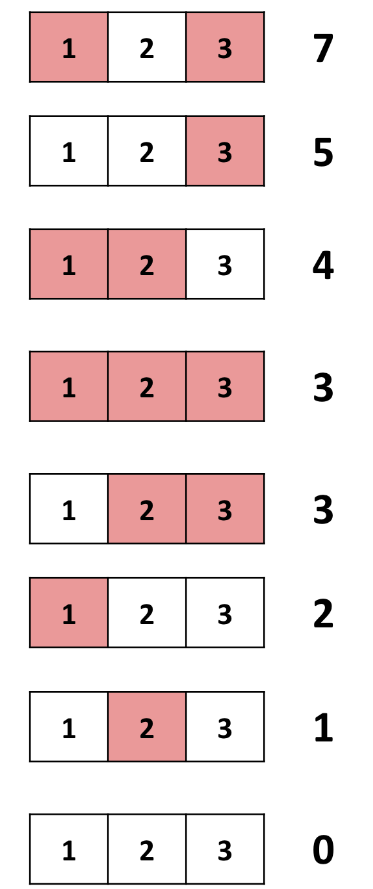
Output
Elsie正在学习绘画。她有一块由n个单元格组成的画布,单元格编号从1到n,她可以选择任意(可能为空)的单元格子集进行涂色。
Elsie有一个2D数组a,她将使用这个数组来评估画作。假设一幅画中涂色的单元格形成的最长连续区间为[l1,r1],[l2,r2],…,[lx,rx],那么这幅画的“美感”就是所有1≤i≤x的a_{l_i,r_i}之和。在上面的图片中,涂色单元格的最长连续区间是[2,4],[6,6],[8,9],因此这幅画的“美感”是a_{2,4}+a_{6,6}+a_{8,9}。
总共有2^n种涂色画布的方式。帮助Elsie找出这2^n种方式中“美感”值最大的k种,注意这k种值不一定要互不相同。保证至少有k种不同的涂色方式。
输入输出数据格式:
输入:
- 第一行包含一个整数t(1≤t≤10^3),表示测试用例的数量。
- 每个测试用例的第一行包含两个整数n和k(1≤n≤10^3,1≤k≤min(2^n, 5*10^3)),分别表示单元格的数量和需要找到的“美感”值最大的k种。
- 接下来的n行描述数组a,其中第i行包含n-i+1个整数a_{i,i},a_{i,i+1},…,a_{i,n}(-10^6≤a_{i,j}≤10^6)。
- 保证所有测试用例中n的总和不超过10^3,k的总和不超过5*10^3。
输出:
- 对于每个测试用例,输出一行k个整数,分别表示Elsie可以获得的“美感”值第i大的值。
示例:
输入:
```
4
1 2
-5
2 4
2 -3
-1
3 8
2 4 3
1 3
5
6 20
0 -6 -3 0 -6 -2
-7 -5 -2 -3 -4
7 0 -9 -4
2 -1 1
1 -2
-6
```
输出:
```
0 -5
2 0 -1 -3
7 5 4 3 3 2 1 0
8 8 7 7 5 5 2 2 1 1 1 1 1 1 0 0 0 0 0 -1
```题目大意: Elsie正在学习绘画。她有一块由n个单元格组成的画布,单元格编号从1到n,她可以选择任意(可能为空)的单元格子集进行涂色。 Elsie有一个2D数组a,她将使用这个数组来评估画作。假设一幅画中涂色的单元格形成的最长连续区间为[l1,r1],[l2,r2],…,[lx,rx],那么这幅画的“美感”就是所有1≤i≤x的a_{l_i,r_i}之和。在上面的图片中,涂色单元格的最长连续区间是[2,4],[6,6],[8,9],因此这幅画的“美感”是a_{2,4}+a_{6,6}+a_{8,9}。 总共有2^n种涂色画布的方式。帮助Elsie找出这2^n种方式中“美感”值最大的k种,注意这k种值不一定要互不相同。保证至少有k种不同的涂色方式。 输入输出数据格式: 输入: - 第一行包含一个整数t(1≤t≤10^3),表示测试用例的数量。 - 每个测试用例的第一行包含两个整数n和k(1≤n≤10^3,1≤k≤min(2^n, 5*10^3)),分别表示单元格的数量和需要找到的“美感”值最大的k种。 - 接下来的n行描述数组a,其中第i行包含n-i+1个整数a_{i,i},a_{i,i+1},…,a_{i,n}(-10^6≤a_{i,j}≤10^6)。 - 保证所有测试用例中n的总和不超过10^3,k的总和不超过5*10^3。 输出: - 对于每个测试用例,输出一行k个整数,分别表示Elsie可以获得的“美感”值第i大的值。 示例: 输入: ``` 4 1 2 -5 2 4 2 -3 -1 3 8 2 4 3 1 3 5 6 20 0 -6 -3 0 -6 -2 -7 -5 -2 -3 -4 7 0 -9 -4 2 -1 1 1 -2 -6 ``` 输出: ``` 0 -5 2 0 -1 -3 7 5 4 3 3 2 1 0 8 8 7 7 5 5 2 2 1 1 1 1 1 1 0 0 0 0 0 -1 ```