311148: CF1941D. Rudolf and the Ball Game
Description
Rudolf and Bernard decided to play a game with their friends. $n$ people stand in a circle and start throwing a ball to each other. They are numbered from $1$ to $n$ in the clockwise order.
Let's call a transition a movement of the ball from one player to his neighbor. The transition can be made clockwise or counterclockwise.
Let's call the clockwise (counterclockwise) distance from player $y_1$ to player $y_2$ the number of transitions clockwise (counterclockwise) that need to be made to move from player $y_1$ to player $y_2$. For example, if $n=7$ then the clockwise distance from $2$ to $5$ is $3$, and the counterclockwise distance from $2$ to $5$ is $4$.
Initially, the ball is with the player number $x$ (players are numbered clockwise). On the $i$-th move the person with the ball throws it at a distance of $r_i$ ($1 \le r_i \le n - 1$) clockwise or counterclockwise. For example, if there are $7$ players, and the $2$nd player, after receiving the ball, throws it a distance of $5$, then the ball will be caught by either the $7$th player (throwing clockwise) or the $4$th player (throwing counterclockwise). An illustration of this example is shown below.
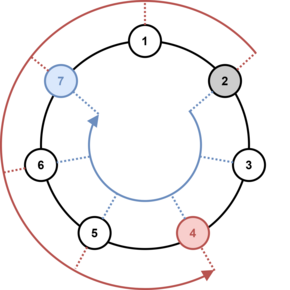
The game was interrupted after $m$ throws due to unexpected rain. When the rain stopped, the guys gathered again to continue. However, no one could remember who had the ball. As it turned out, Bernard remembered the distances for each of the throws and the direction for some of the throws (clockwise or counterclockwise).
Rudolf asks you to help him and based on the information from Bernard, calculate the numbers of the players who could have the ball after $m$ throws.
InputThe first line of the input contains a single integer $t$ ($1 \le t \le 10^4$) — the number of test cases. Then follow the descriptions of the test cases.
The first line of each test case contains three integers $n, m, x$ ($2 \le n \le 1000$, $1 \le m \le 1000$, $1 \le x \le n$) — the number of players, the number of throws made, and the number of the player who threw the ball first, respectively.
The next $m$ lines contain information about each throw in order. Each of them contains an integer $r_i$ ($1 \le r_i \le n - 1$) — the distance at which the $i$-th throw was made, and a symbol $c_i$, equal to '0', '1', or '?':
- if $c_i$='0', then the $i$-th throw was made clockwise,
- if $c_i$='1', then the $i$-th throw was made counterclockwise,
- if $c_i$='?', then Bernard does not remember the direction and the $i$-th throw could have been made either clockwise or counterclockwise.
It is guaranteed that the sum $n \cdot m$ ($n$ multiplied by $m$) over all test cases does not exceed $2 \cdot 10^5$.
OutputFor each test case, output two lines.
In the first line, output the number of players $k$ ($1 \le k \le n$) who could have the ball at the end of the game.
In the next line, output $k$ numbers $b_i$ ($1 \le b_i \le n$) — the numbers of the players in increasing order. All numbers must be different.
ExampleInput5 6 3 2 2 ? 2 ? 2 ? 12 1 2 3 1 10 7 4 2 ? 9 1 4 ? 7 0 2 0 8 1 5 ? 5 3 1 4 0 4 ? 1 ? 4 1 1 2 ?Output
3 2 4 6 1 11 4 3 5 7 9 3 2 3 5 1 3Note
Below is an illustration of three throws for the first test case. The arrows denote possible throw directions. Players who could have the ball after the throw are highlighted in gray.
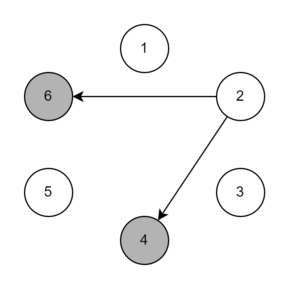
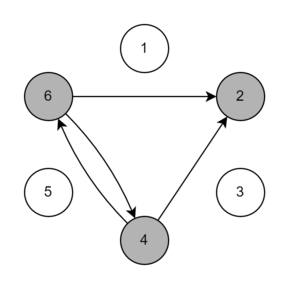
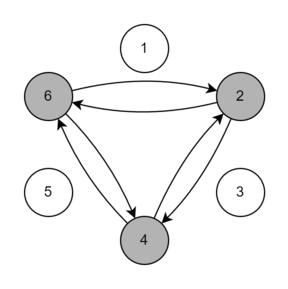
Output
定义:从一个玩家y1到另一个玩家y2的顺时针(逆时针)距离是需要顺时针(逆时针)移动的次数。例如,如果n=7,那么从2到5的顺时针距离是3,逆时针距离是4。
最初,球在编号为x的玩家手中(玩家按顺时针编号)。在第i次移动中,持球的玩家将球顺时针或逆时针扔出r_i的距离(1≤r_i≤n-1)。例如,如果有7个玩家,第二个玩家在接到球后,扔出5的距离,那么球会被第七个玩家(顺时针)或第四个玩家(逆时针)接住。
游戏在进行m次投掷后因为意外降雨而中断。雨停后,大家又聚在一起继续玩,但是没有人记得球在谁手里。结果显示,伯纳德记住了每次投掷的距离,以及部分投掷的方向(顺时针或逆时针)。
鲁道夫请你帮助他,根据伯纳德的信息,计算在m次投掷后可能持有球的玩家编号。
输入输出数据格式:
输入:
- 第一行包含一个整数t(1≤t≤10^4),表示测试用例的数量。
- 每个测试用例的第一行包含三个整数n, m, x(2≤n≤1000,1≤m≤1000,1≤x≤n),分别表示玩家数量、进行的投掷次数和首先投掷的玩家编号。
- 接下来的m行,每行包含一个整数r_i(1≤r_i≤n-1),表示第i次投掷的距离,以及一个字符c_i,c_i可以是'0'、'1'或'?':
- 如果c_i='0',则第i次投掷是顺时针的;
- 如果c_i='1',则第i次投掷是逆时针的;
- 如果c_i='?',则伯纳德不记得方向,第i次投掷可能是顺时针或逆时针。
保证所有测试用例的n*m之和不超过2*10^5。
输出:
- 对于每个测试用例,输出两行。
- 第一行输出一个整数k(1≤k≤n),表示可能最后持有球的玩家数量。
- 第二行输出k个不同的整数b_i(1≤b_i≤n),表示可能最后持有球的玩家的编号,按升序排列。
示例输入输出已给出。题目大意:鲁道夫和伯纳德决定和朋友们玩一个游戏。有n个人站成一个圈,开始互相扔球。他们按顺时针方向从1到n编号。 定义:从一个玩家y1到另一个玩家y2的顺时针(逆时针)距离是需要顺时针(逆时针)移动的次数。例如,如果n=7,那么从2到5的顺时针距离是3,逆时针距离是4。 最初,球在编号为x的玩家手中(玩家按顺时针编号)。在第i次移动中,持球的玩家将球顺时针或逆时针扔出r_i的距离(1≤r_i≤n-1)。例如,如果有7个玩家,第二个玩家在接到球后,扔出5的距离,那么球会被第七个玩家(顺时针)或第四个玩家(逆时针)接住。 游戏在进行m次投掷后因为意外降雨而中断。雨停后,大家又聚在一起继续玩,但是没有人记得球在谁手里。结果显示,伯纳德记住了每次投掷的距离,以及部分投掷的方向(顺时针或逆时针)。 鲁道夫请你帮助他,根据伯纳德的信息,计算在m次投掷后可能持有球的玩家编号。 输入输出数据格式: 输入: - 第一行包含一个整数t(1≤t≤10^4),表示测试用例的数量。 - 每个测试用例的第一行包含三个整数n, m, x(2≤n≤1000,1≤m≤1000,1≤x≤n),分别表示玩家数量、进行的投掷次数和首先投掷的玩家编号。 - 接下来的m行,每行包含一个整数r_i(1≤r_i≤n-1),表示第i次投掷的距离,以及一个字符c_i,c_i可以是'0'、'1'或'?': - 如果c_i='0',则第i次投掷是顺时针的; - 如果c_i='1',则第i次投掷是逆时针的; - 如果c_i='?',则伯纳德不记得方向,第i次投掷可能是顺时针或逆时针。 保证所有测试用例的n*m之和不超过2*10^5。 输出: - 对于每个测试用例,输出两行。 - 第一行输出一个整数k(1≤k≤n),表示可能最后持有球的玩家数量。 - 第二行输出k个不同的整数b_i(1≤b_i≤n),表示可能最后持有球的玩家的编号,按升序排列。 示例输入输出已给出。