311098: CF1933F. Turtle Mission: Robot and the Earthquake
Description
The world is a grid with $n$ rows and $m$ columns. The rows are numbered $0, 1, \ldots, n-1$, while the columns are numbered $0, 1, \ldots, m-1$. In this world, the columns are cyclic (i.e. the top and the bottom cells in each column are adjacent). The cell on the $i$-th row and the $j$-th column ($0 \le i < n, 0 \le j < m$) is denoted as $(i,j)$.
At time $0$, the cell $(i,j)$ (where $0 \le i < n, 0 \le j < m$) contains either a rock or nothing. The state of cell $(i,j)$ can be described using the integer $a_{i,j}$:
- If $a_{i,j} = 1$, there is a rock at $(i,j)$.
- If $a_{i,j} = 0$, there is nothing at $(i,j)$.
As a result of aftershocks from the earthquake, the columns follow tectonic plate movements: each column moves cyclically upwards at a velocity of $1$ cell per unit of time. Formally, for some $0 \le i < n, 0 \le j < m$, if $(i,j)$ contains a rock at the moment, it will move from $(i, j)$ to $(i - 1, j)$ (or to $(n - 1, j)$ if $i=0$).
The robot called RT is initially positioned at $(0,0)$. It has to go to $(n-1,m-1)$ to carry out an earthquake rescue operation (to the bottom rightmost cell). The earthquake doesn't change the position of the robot, they only change the position of rocks in the world.
Let RT's current position be $(x,y)$ ($0 \le x < n, 0 \le y < m$), it can perform the following operations:
- Go one cell cyclically upwards, i.e. from $(x,y)$ to $((x+n-1) \bmod n, y)$ using $1$ unit of time.
- Go one cell cyclically downwards, i.e. $(x,y)$ to $((x+1) \bmod n, y)$ using $1$ unit of time.
- Go one cell to the right, i.e. $(x,y)$ to $(x, y+1)$ using $1$ unit of time. (RT may perform this operation only if $y < m-1$.)
Note that RT cannot go left using the operations nor can he stay at a position.
Unfortunately, RT will explode upon colliding with a rock. As such, when RT is at $(x,y)$ and there is a rock at $((x+1) \bmod n, y)$ or $((x+2) \bmod n, y)$, RT cannot move down or it will be hit by the rock.
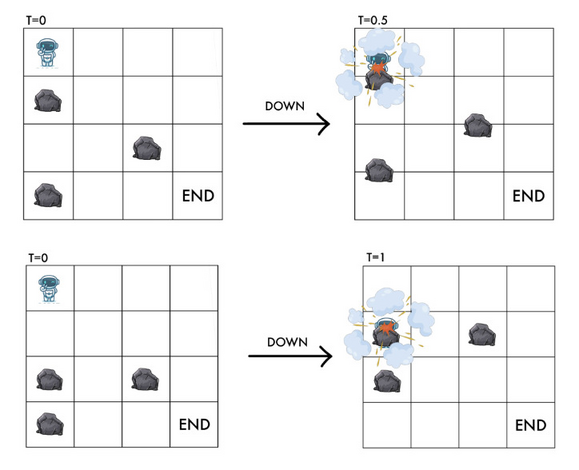
Similarly, if $y+1 < m$ and there is a rock at $((x+1) \bmod n, y+1)$, RT cannot move right or it will be hit by the rock.
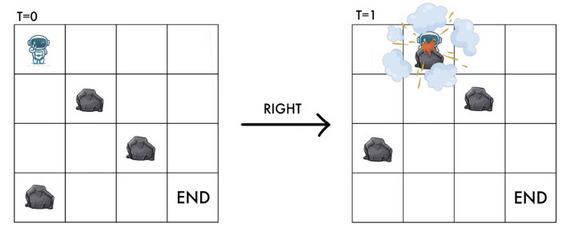
However, it is worth noting that if there is a rock at $(x \bmod n, y+1)$ and $((x+1) \bmod n, y)$, RT can still move right safely.
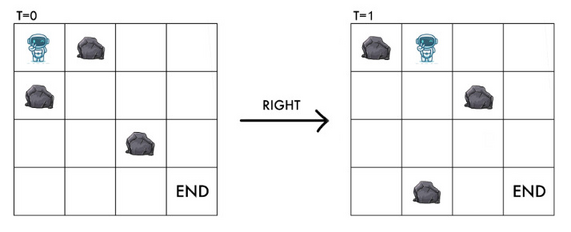
Find the minimum amount of time RT needs to reach $(n-1,m-1)$ without colliding with any rocks. If it is impossible to do so, output $-1$.
InputThe first line of the input contains one integer $t$ ($1 \le t \le 10^4$) — the number of test cases.
In each test case, the first line contains two integers $n$, $m$ ($3 \le n, m \le 10^3$) — the size of the planet's boundaries.
Each of the next $n$ lines contains $m$ integers. The $(j+1)$-th integer on the $(i+1)$-th line ($0 \le i < n, 0 \le j < m$) is $a_{i,j}$ ($0 \le a_{i,j} \le 1$), which denotes whether or not there is a rock at $(i,j)$ at time $0$.
Additionally, it is guaranteed that $a_{0,0} = 0$, and $a_{i, m-1} = 0$ for $0 \le i < n$. In other words, there is no rock at RT's initial position as well as column $m-1$.
The sum of $n \cdot m$ over all test cases does not exceed $10^6$.
OutputFor each test case:
- If the destination can be reached without colliding with any rocks, output a single integer — the minimum amount of time RT needs to reach $(n-1,m-1)$.
- Otherwise, output $-1$.
6 4 5 0 1 0 0 0 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 3 3 0 0 0 1 0 0 0 0 0 5 3 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 3 7 0 0 1 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 3 4 0 1 0 0 1 0 0 0 0 1 1 0 5 5 0 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 0 0 0 0 1 0Output
7 3 3 8 -1 12Input
6 3 3 0 0 0 0 0 0 0 0 0 4 3 0 1 0 1 0 0 0 1 0 1 0 0 4 3 0 1 0 0 1 0 0 1 0 0 1 0 3 3 0 0 0 1 1 0 0 0 0 3 3 0 1 0 0 0 0 0 1 0 5 5 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0Output
3 3 -1 -1 3 8Note
Visual explanation of the first test case in the example:
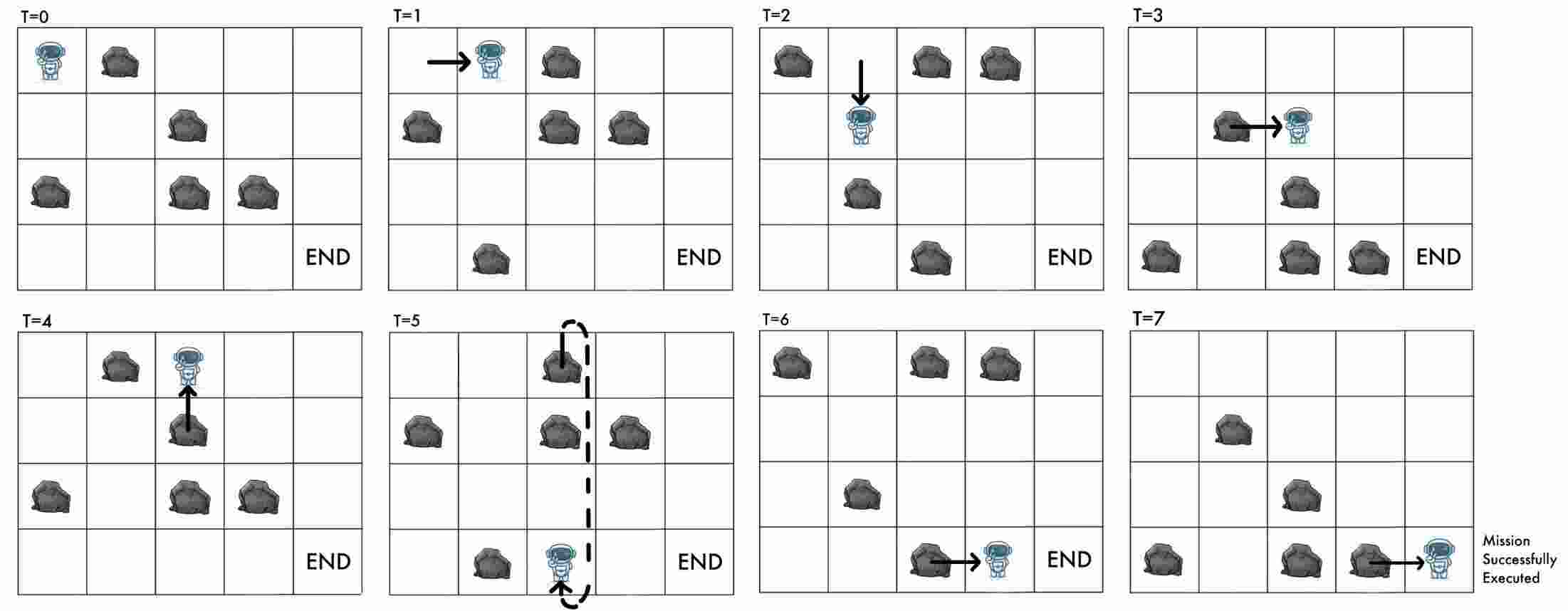
Output
在一个有 $ n $ 行 $ m $ 列的网格世界中,列是循环的(即每列的顶部和底部单元格是相邻的)。每个单元格 $ (i, j) $ ($ 0 \leq i < n, 0 \leq j < m $)在时间 $ 0 $ 时包含一个石头或什么也没有。石头的状态用整数 $ a_{i,j} $ 描述:如果 $ a_{i,j} = 1 $,则表示有石头;如果 $ a_{i,j} = 0 $,则表示没有石头。
由于地震的余震,列会按照板块运动循环向上移动,速度为每单位时间移动一个单元格。如果单元格 $ (i,j) $ 在某时刻有石头,它会从 $ (i, j) $ 移动到 $ (i - 1, j) $(如果 $ i = 0 $ 则移动到 $ (n - 1, j) $)。
机器人 RT 初始位于 $ (0,0) $,必须到达 $ (n-1, m-1) $ 以执行地震救援任务。地震不会改变机器人的位置,只会改变世界中石头的位置。
RT 的当前位置为 $ (x, y) $,可以执行以下操作:
1. 循环向上移动一个单元格,从 $ (x, y) $ 到 $ ((x+n-1) \mod n, y) $,使用 1 个单位时间。
2. 循环向下移动一个单元格,从 $ (x, y) $ 到 $ ((x+1) \mod n, y) $,使用 1 个单位时间。
3. 向右移动一个单元格,从 $ (x, y) $ 到 $ (x, y+1) $,使用 1 个单位时间。(RT 只能在 $ y < m-1 $ 时执行此操作)
注意,RT 不能向左移动,也不能停留在原地。
如果 RT 在 $ (x, y) $ 时,$ ((x+1) \mod n, y) $ 或 $ ((x+2) \mod n, y) $ 处有石头,RT 不能向下移动,否则会被石头击中。同样,如果 $ y+1 < m $ 且 $ ((x+1) \mod n, y+1) $ 处有石头,RT 不能向右移动。
输入输出数据格式:
输入:
- 第一行包含一个整数 $ t $($ 1 \leq t \leq 10^4 $),表示测试用例的数量。
- 每个测试用例的第一行包含两个整数 $ n, m $($ 3 \leq n, m \leq 10^3 $),表示行星边界的尺寸。
- 接下来的 $ n $ 行,每行包含 $ m $ 个整数,表示每个单元格在时间 $ 0 $ 时是否含有石头。
- 保证 $ a_{0,0} = 0 $,且对于 $ 0 \leq i < n $,有 $ a_{i, m-1} = 0 $,即 RT 的初始位置和列 $ m-1 $ 上没有石头。
- 所有测试用例的 $ n \cdot m $ 之和不超过 $ 10^6 $。
输出:
- 对于每个测试用例,如果可以不与任何石头碰撞到达 $ (n-1, m-1) $,则输出一个整数,表示 RT 到达目的地所需的最小时间;否则输出 -1。
示例:
输入:
```
6
4 5
0 1 0 0 0
0 0 1 0 0
1 0 1 1 0
0 0 0 0 0
3 3
0 0 0
1 0 0
0 0 0
5 3
0 0 0
0 0 0
1 0 0
0 0 0
1 0 0
3 7
0 0 1 0 0 1 0
1 0 1 0 1 0 0
0 1 0 0 0 0 0
3 4
0 1 0 0
1 0 0 0
0 1 1 0
5 5
0 0 0 0 0
0 1 0 1 0
0 1 0 1 0
0 1 0 1 0
0 0 0 1 0
```
输出:
```
7
3
3
8
-1
12
```题目大意: 在一个有 $ n $ 行 $ m $ 列的网格世界中,列是循环的(即每列的顶部和底部单元格是相邻的)。每个单元格 $ (i, j) $ ($ 0 \leq i < n, 0 \leq j < m $)在时间 $ 0 $ 时包含一个石头或什么也没有。石头的状态用整数 $ a_{i,j} $ 描述:如果 $ a_{i,j} = 1 $,则表示有石头;如果 $ a_{i,j} = 0 $,则表示没有石头。 由于地震的余震,列会按照板块运动循环向上移动,速度为每单位时间移动一个单元格。如果单元格 $ (i,j) $ 在某时刻有石头,它会从 $ (i, j) $ 移动到 $ (i - 1, j) $(如果 $ i = 0 $ 则移动到 $ (n - 1, j) $)。 机器人 RT 初始位于 $ (0,0) $,必须到达 $ (n-1, m-1) $ 以执行地震救援任务。地震不会改变机器人的位置,只会改变世界中石头的位置。 RT 的当前位置为 $ (x, y) $,可以执行以下操作: 1. 循环向上移动一个单元格,从 $ (x, y) $ 到 $ ((x+n-1) \mod n, y) $,使用 1 个单位时间。 2. 循环向下移动一个单元格,从 $ (x, y) $ 到 $ ((x+1) \mod n, y) $,使用 1 个单位时间。 3. 向右移动一个单元格,从 $ (x, y) $ 到 $ (x, y+1) $,使用 1 个单位时间。(RT 只能在 $ y < m-1 $ 时执行此操作) 注意,RT 不能向左移动,也不能停留在原地。 如果 RT 在 $ (x, y) $ 时,$ ((x+1) \mod n, y) $ 或 $ ((x+2) \mod n, y) $ 处有石头,RT 不能向下移动,否则会被石头击中。同样,如果 $ y+1 < m $ 且 $ ((x+1) \mod n, y+1) $ 处有石头,RT 不能向右移动。 输入输出数据格式: 输入: - 第一行包含一个整数 $ t $($ 1 \leq t \leq 10^4 $),表示测试用例的数量。 - 每个测试用例的第一行包含两个整数 $ n, m $($ 3 \leq n, m \leq 10^3 $),表示行星边界的尺寸。 - 接下来的 $ n $ 行,每行包含 $ m $ 个整数,表示每个单元格在时间 $ 0 $ 时是否含有石头。 - 保证 $ a_{0,0} = 0 $,且对于 $ 0 \leq i < n $,有 $ a_{i, m-1} = 0 $,即 RT 的初始位置和列 $ m-1 $ 上没有石头。 - 所有测试用例的 $ n \cdot m $ 之和不超过 $ 10^6 $。 输出: - 对于每个测试用例,如果可以不与任何石头碰撞到达 $ (n-1, m-1) $,则输出一个整数,表示 RT 到达目的地所需的最小时间;否则输出 -1。 示例: 输入: ``` 6 4 5 0 1 0 0 0 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 3 3 0 0 0 1 0 0 0 0 0 5 3 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 3 7 0 0 1 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 3 4 0 1 0 0 1 0 0 0 0 1 1 0 5 5 0 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 0 0 0 0 1 0 ``` 输出: ``` 7 3 3 8 -1 12 ```