311068: CF1929F. Sasha and the Wedding Binary Search Tree

F. Sasha and the Wedding Binary Search Treetime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Having overcome all the difficulties and hardships, Sasha finally decided to marry his girlfriend. To do this, he needs to give her an engagement ring. However, his girlfriend does not like such romantic gestures, but she does like binary search trees$^{\dagger}$. So Sasha decided to give her such a tree.

After spending a lot of time on wedding websites for programmers, he found the perfect binary search tree with the root at vertex $1$. In this tree, the value at vertex $v$ is equal to $val_v$.

But after some time, he forgot the values in some vertices. Trying to remember the found tree, Sasha wondered — how many binary search trees could he have found on the website, if it is known that the values in all vertices are integers in the segment $[1, C]$. Since this number can be very large, output it modulo $998\,244\,353$.

$^{\dagger}$A binary search tree is a rooted binary tree in which for any vertex $x$, the following property holds: the values of all vertices in the left subtree of vertex $x$ (if it exists) are less than or equal to the value at vertex $x$, and the values of all vertices in the right subtree of vertex $x$ (if it exists) are greater than or equal to the value at vertex $x$.

Input

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^5$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains two integers $n$ and $C$ ($2 \leq n \leq 5 \cdot 10^5$, $1 \leq C \leq 10^9$) — the number of vertices in the tree and the maximum allowed value at the vertex.

The next $n$ lines describe the vertices of the tree. The $i$-th line contains three integers $L_i, R_i$ and $val_i$ ($-1 \le L_i, R_i \le n$, $-1 \le val_i \le C$, $L_i, R_i, val_i \ne 0$) — the number of the left child, the number of the right child, and the value at the $i$-th vertex, respectively. If $L_i = -1$, then the $i$-th vertex has no left son. If $R_i = -1$, then the $i$-th vertex has no right son. If $val_i = -1$, then the value at the $i$-th vertex is unknown.

It is guaranteed that at least one suitable binary search tree exists.

It is guaranteed that the sum of $n$ over all test cases does not exceed $5 \cdot 10^5$.

Output

For each test case, output a single integer — the number of suitable binary search trees modulo $998\,244\,353$.

ExampleInput

3
5 5
2 3 -1
-1 -1 2
4 -1 3
-1 5 -1
-1 -1 -1
3 69
2 3 47
-1 -1 13
-1 -1 69
3 3
2 3 -1
-1 -1 -1
-1 -1 -1

Output

4
1
10

Note

In the first test case, the binary search tree has the following form:

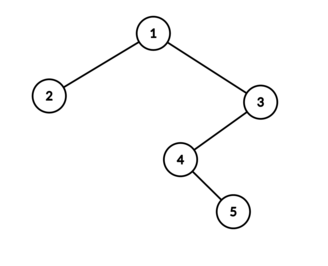
Then the possible values at the vertices are: $[2, 2, 3, 2, 2]$, $[2, 2, 3, 2, 3]$, $[2, 2, 3, 3, 3]$, and $[3, 2, 3, 3, 3]$.

In the second test case, the values at all vertices are known, so there is only one suitable binary search tree.

题目大意：
Sasha 决定与他的女朋友结婚，女朋友不喜欢浪漫的求婚戒指，但她喜欢二叉搜索树。Sasha 在程序员的婚礼网站上找到了一个完美的二叉搜索树，其根节点为 1。在这个树中，节点 v 的值为 val_v。但他忘记了一些节点的值。Sasha 想知道，如果所有节点的值都是区间 [1, C] 中的整数，他可能在该网站上找到多少这样的二叉搜索树。由于这个数字可能非常大，所以结果需要模 998,244,353 输出。

输入输出数据格式：
输入：
- 第一行包含一个整数 t (1 ≤ t ≤ 10^5)，表示测试用例的数量。
- 每个测试用例的第一行包含两个整数 n 和 C (2 ≤ n ≤ 5 × 10^5, 1 ≤ C ≤ 10^9)，分别表示树中节点的数量和节点的最大允许值。
- 接下来的 n 行描述了树的节点。第 i 行包含三个整数 L_i, R_i 和 val_i (-1 ≤ L_i, R_i ≤ n, -1 ≤ val_i ≤ C, L_i, R_i, val_i ≠ 0)，分别表示第 i 个节点的左孩子编号、右孩子编号和该节点的值。如果 L_i = -1，则第 i 个节点没有左孩子；如果 R_i = -1，则没有右孩子；如果 val_i = -1，则该节点的值未知。
- 保证至少存在一个合适的二叉搜索树。
- 保证所有测试用例的 n 之和不超过 5 × 10^5。

输出：
- 对于每个测试用例，输出一个整数，表示合适的二叉搜索树的数量，模 998,244,353。

示例：
输入：
```
3
5 5
2 3 -1
-1 -1 2
4 -1 3
-1 5 -1
-1 -1 -1
3 69
2 3 47
-1 -1 13
-1 -1 69
3 3
2 3 -1
-1 -1 -1
-1 -1 -1
```
输出：
```
4
1
10
```

注意：
- 在第一个测试用例中，二叉搜索树的可能值有：[2, 2, 3, 2, 2], [2, 2, 3, 2, 3], [2, 2, 3, 3, 3], 和 [3, 2, 3, 3, 3]。
- 在第二个测试用例中，所有节点的值都已知，因此只有一个合适的二叉搜索树。题目大意： Sasha 决定与他的女朋友结婚，女朋友不喜欢浪漫的求婚戒指，但她喜欢二叉搜索树。Sasha 在程序员的婚礼网站上找到了一个完美的二叉搜索树，其根节点为 1。在这个树中，节点 v 的值为 val_v。但他忘记了一些节点的值。Sasha 想知道，如果所有节点的值都是区间 [1, C] 中的整数，他可能在该网站上找到多少这样的二叉搜索树。由于这个数字可能非常大，所以结果需要模 998,244,353 输出。 输入输出数据格式： 输入： - 第一行包含一个整数 t (1 ≤ t ≤ 10^5)，表示测试用例的数量。 - 每个测试用例的第一行包含两个整数 n 和 C (2 ≤ n ≤ 5 × 10^5, 1 ≤ C ≤ 10^9)，分别表示树中节点的数量和节点的最大允许值。 - 接下来的 n 行描述了树的节点。第 i 行包含三个整数 L_i, R_i 和 val_i (-1 ≤ L_i, R_i ≤ n, -1 ≤ val_i ≤ C, L_i, R_i, val_i ≠ 0)，分别表示第 i 个节点的左孩子编号、右孩子编号和该节点的值。如果 L_i = -1，则第 i 个节点没有左孩子；如果 R_i = -1，则没有右孩子；如果 val_i = -1，则该节点的值未知。 - 保证至少存在一个合适的二叉搜索树。 - 保证所有测试用例的 n 之和不超过 5 × 10^5。 输出： - 对于每个测试用例，输出一个整数，表示合适的二叉搜索树的数量，模 998,244,353。 示例： 输入： ``` 3 5 5 2 3 -1 -1 -1 2 4 -1 3 -1 5 -1 -1 -1 -1 3 69 2 3 47 -1 -1 13 -1 -1 69 3 3 2 3 -1 -1 -1 -1 -1 -1 -1 ``` 输出： ``` 4 1 10 ``` 注意： - 在第一个测试用例中，二叉搜索树的可能值有：[2, 2, 3, 2, 2], [2, 2, 3, 2, 3], [2, 2, 3, 3, 3], 和 [3, 2, 3, 3, 3]。 - 在第二个测试用例中，所有节点的值都已知，因此只有一个合适的二叉搜索树。