311066: CF1929D. Sasha and a Walk in the City

D. Sasha and a Walk in the Citytime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Sasha wants to take a walk with his girlfriend in the city. The city consists of $n$ intersections, numbered from $1$ to $n$. Some of them are connected by roads, and from any intersection, there is exactly one simple path$^{\dagger}$ to any other intersection. In other words, the intersections and the roads between them form a tree.

Some of the intersections are considered dangerous. Since it is unsafe to walk alone in the city, Sasha does not want to visit three or more dangerous intersections during the walk.

Sasha calls a set of intersections good if the following condition is satisfied:

• If in the city only the intersections contained in this set are dangerous, then any simple path in the city contains no more than two dangerous intersections.

However, Sasha does not know which intersections are dangerous, so he is interested in the number of different good sets of intersections in the city. Since this number can be very large, output it modulo $998\,244\,353$.

$^{\dagger}$A simple path is a path that passes through each intersection at most once.

Input

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2 \le n \leq 3 \cdot 10^5$) — the number of intersections in the city.

The next $(n - 1)$ lines describe the roads. The $i$-th line contains two integers $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq n$, $u_i \ne v_i$) — the numbers of the intersections connected by the $i$-th road.

It is guaranteed that these roads form a tree.

It is guaranteed that the sum of $n$ over all test cases does not exceed $3 \cdot 10^5$.

Output

For each test case, output a single integer — the number of good sets of intersections modulo $998\,244\,353$.

ExampleInput

4
3
1 3
3 2
4
3 4
2 3
3 1
5
1 2
3 4
5 1
2 3
4
1 2
2 3
3 4

Output

7
12
16
11

Note

In the first test case, there are $2^3 = 8$ sets of intersections. All of them are good, except for the set $\{1, 2, 3\}$, because if intersections $1, 2$, and $3$ are dangerous, then the simple path $1 - 2 - 3$ contains $3$ dangerous intersections. Thus, there are $7$ good sets.

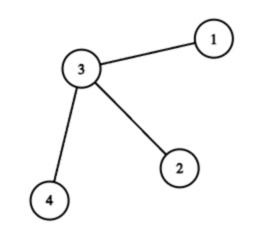
In the second test case, there are $2^4 = 16$ sets of intersections. Among them, the sets $\{1, 2, 3, 4\}$, $\{1, 2, 3\}$, $\{1, 3, 4\}$, $\{2, 3, 4\}$ are not good. Thus, there are a total of $12$ good sets. The city layout is shown below:

题目大意：
Sasha 想要和他的女朋友在城市里散步。城市由 n 个路口组成，编号从 1 到 n。其中一些路口通过道路相连，且从任一路口出发，到其他任一路口都存在唯一的简单路径。换句话说，路口和它们之间的道路形成了一棵树。一些路口被认为是危险的。由于独自一人在城市中行走是不安全的，Sasha 不想在他的散步中经过三个或更多的危险路口。Sasha 称一组路口为“好的”，如果满足以下条件：如果城市中只有包含在这个集合中的路口是危险的，那么城市中的任何简单路径都不包含超过两个危险路口。然而，Sasha 不知道哪些路口是危险的，所以他对于城市中不同“好的”路口集合的数量感兴趣。由于这个数字可能非常大，所以结果需要模上 998,244,353 输出。

输入输出数据格式：
输入：
- 第一行包含一个整数 t（1 ≤ t ≤ 10^4），表示测试用例的数量。
- 每个测试用例的第一行包含一个整数 n（2 ≤ n ≤ 3 × 10^5），表示城市中路口的数量。
- 接下来的 n-1 行描述了道路。第 i 行包含两个整数 u_i 和 v_i（1 ≤ u_i, v_i ≤ n，u_i ≠ v_i），表示第 i 条道路连接的两个路口的编号。
- 保证这些道路构成一棵树。
- 保证所有测试用例中 n 的总和不超过 3 × 10^5。

输出：
- 对于每个测试用例，输出一个整数，表示城市中“好的”路口集合的数量，模上 998,244,353。

示例：
输入：
```
4
3
1 3
3 2
4
3 4
2 3
3 1
5
1 2
3 4
5 1
2 3
4
1 2
2 3
3 4
```
输出：
```
7
12
16
11
```题目大意： Sasha 想要和他的女朋友在城市里散步。城市由 n 个路口组成，编号从 1 到 n。其中一些路口通过道路相连，且从任一路口出发，到其他任一路口都存在唯一的简单路径。换句话说，路口和它们之间的道路形成了一棵树。一些路口被认为是危险的。由于独自一人在城市中行走是不安全的，Sasha 不想在他的散步中经过三个或更多的危险路口。Sasha 称一组路口为“好的”，如果满足以下条件：如果城市中只有包含在这个集合中的路口是危险的，那么城市中的任何简单路径都不包含超过两个危险路口。然而，Sasha 不知道哪些路口是危险的，所以他对于城市中不同“好的”路口集合的数量感兴趣。由于这个数字可能非常大，所以结果需要模上 998,244,353 输出。 输入输出数据格式： 输入： - 第一行包含一个整数 t（1 ≤ t ≤ 10^4），表示测试用例的数量。 - 每个测试用例的第一行包含一个整数 n（2 ≤ n ≤ 3 × 10^5），表示城市中路口的数量。 - 接下来的 n-1 行描述了道路。第 i 行包含两个整数 u_i 和 v_i（1 ≤ u_i, v_i ≤ n，u_i ≠ v_i），表示第 i 条道路连接的两个路口的编号。 - 保证这些道路构成一棵树。 - 保证所有测试用例中 n 的总和不超过 3 × 10^5。 输出： - 对于每个测试用例，输出一个整数，表示城市中“好的”路口集合的数量，模上 998,244,353。 示例： 输入： ``` 4 3 1 3 3 2 4 3 4 2 3 3 1 5 1 2 3 4 5 1 2 3 4 1 2 2 3 3 4 ``` 输出： ``` 7 12 16 11 ```