311057: CF1928A. Rectangle Cutting

A. Rectangle Cuttingtime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Bob has a rectangle of size $a \times b$. He tries to cut this rectangle into two rectangles with integer sides by making a cut parallel to one of the sides of the original rectangle. Then Bob tries to form some other rectangle from the two resulting rectangles, and he can rotate and move these two rectangles as he wishes.

Note that if two rectangles differ only by a $90^{\circ}$ rotation, they are considered the same. For example, the rectangles $6 \times 4$ and $4 \times 6$ are considered the same.

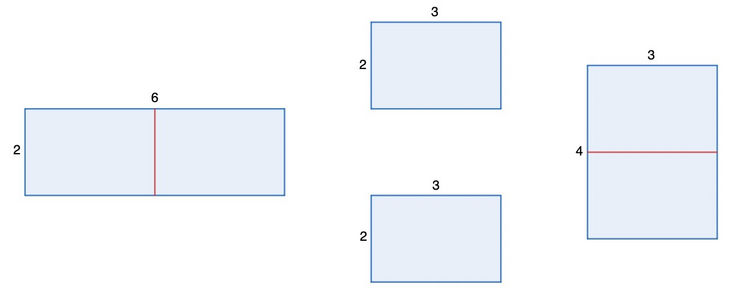
Thus, from the $2 \times 6$ rectangle, another rectangle can be formed, because it can be cut into two $2 \times 3$ rectangles, and then these two rectangles can be used to form the $4 \times 3$ rectangle, which is different from the $2 \times 6$ rectangle.

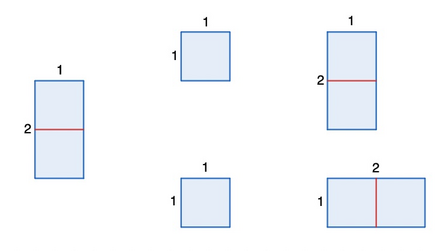
However, from the $2 \times 1$ rectangle, another rectangle cannot be formed, because it can only be cut into two rectangles of $1 \times 1$, and from these, only the $1 \times 2$ and $2 \times 1$ rectangles can be formed, which are considered the same.

Help Bob determine if he can obtain some other rectangle, or if he is just wasting his time.

Input

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases. This is followed by the description of the test cases.

The single line of each test case contains two integers $a$ and $b$ ($1 \le a, b \le 10^9$) — the size of Bob's rectangle.

Output

For each test case, output "Yes" if Bob can obtain another rectangle from the $a \times b$ rectangle. Otherwise, output "No".

You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive answers.

ExampleInput

7
1 1
2 1
2 6
3 2
2 2
2 4
6 3

Output

No
No
Yes
Yes
Yes
Yes
No

Note

In the first test case, the $1 \times 1$ rectangle cannot be cut into two rectangles, so another rectangle cannot be obtained from it.

In the fourth test case, the $3 \times 2$ rectangle can be cut into two $3 \times 1$ rectangles, and from these, the $1 \times 6$ rectangle can be formed.

In the fifth test case, the $2 \times 2$ rectangle can be cut into two $1 \times 2$ rectangles, and from these, the $1 \times 4$ rectangle can be formed.

题目大意：
鲍勃有一个尺寸为 $a \times b$ 的矩形。他试图通过平行于原矩形的一个边来切割这个矩形，将其分成两个整数边长的矩形。然后，鲍勃尝试用这两个结果矩形来形成另一个矩形，他可以任意旋转和移动这两个矩形。

注意，如果两个矩形仅通过 $90^\circ$ 旋转而不同，它们被认为是相同的。例如，$6 \times 4$ 和 $4 \times 6$ 的矩形被认为是相同的。

因此，从 $2 \times 6$ 的矩形可以形成另一个矩形，因为它可以被切割成两个 $2 \times 3$ 的矩形，然后可以用这两个矩形来形成 $4 \times 3$ 的矩形，这与 $2 \times 6$ 的矩形不同。

然而，从 $2 \times 1$ 的矩形无法形成另一个矩形，因为它只能被切割成两个 $1 \times 1$ 的矩形，并且只能用这些矩形形成 $1 \times 2$ 和 $2 \times 1$ 的矩形，它们被认为是相同的。

帮助鲍勃确定他是否能够从 $a \times b$ 的矩形获得另一个矩形，或者他只是在浪费时间。

输入输出数据格式：
每个测试包含多个测试用例。第一行包含一个整数 $t$ ($1 \leq t \leq 10^4$) —— 测试用例的数量。接下来是测试用例的描述。

每个测试用例的单行包含两个整数 $a$ 和 $b$ ($1 \le a, b \le 10^9$) —— 鲍勃的矩形的尺寸。

对于每个测试用例，如果鲍勃可以从 $a \times b$ 的矩形获得另一个矩形，则输出 "Yes"。否则，输出 "No"。

你可以以任何大小写输出答案。例如，字符串 "yEs"、"yes"、"Yes" 和 "YES" 都将被识别为肯定答案。题目大意： 鲍勃有一个尺寸为 $a \times b$ 的矩形。他试图通过平行于原矩形的一个边来切割这个矩形，将其分成两个整数边长的矩形。然后，鲍勃尝试用这两个结果矩形来形成另一个矩形，他可以任意旋转和移动这两个矩形。 注意，如果两个矩形仅通过 $90^\circ$ 旋转而不同，它们被认为是相同的。例如，$6 \times 4$ 和 $4 \times 6$ 的矩形被认为是相同的。 因此，从 $2 \times 6$ 的矩形可以形成另一个矩形，因为它可以被切割成两个 $2 \times 3$ 的矩形，然后可以用这两个矩形来形成 $4 \times 3$ 的矩形，这与 $2 \times 6$ 的矩形不同。 然而，从 $2 \times 1$ 的矩形无法形成另一个矩形，因为它只能被切割成两个 $1 \times 1$ 的矩形，并且只能用这些矩形形成 $1 \times 2$ 和 $2 \times 1$ 的矩形，它们被认为是相同的。 帮助鲍勃确定他是否能够从 $a \times b$ 的矩形获得另一个矩形，或者他只是在浪费时间。 输入输出数据格式： 每个测试包含多个测试用例。第一行包含一个整数 $t$ ($1 \leq t \leq 10^4$) —— 测试用例的数量。接下来是测试用例的描述。 每个测试用例的单行包含两个整数 $a$ 和 $b$ ($1 \le a, b \le 10^9$) —— 鲍勃的矩形的尺寸。 对于每个测试用例，如果鲍勃可以从 $a \times b$ 的矩形获得另一个矩形，则输出 "Yes"。否则，输出 "No"。 你可以以任何大小写输出答案。例如，字符串 "yEs"、"yes"、"Yes" 和 "YES" 都将被识别为肯定答案。