311049: CF1926G. Vlad and Trouble at MIT
Description
Vladislav has a son who really wanted to go to MIT. The college dormitory at MIT (Moldova Institute of Technology) can be represented as a tree with $n$ vertices, each vertex being a room with exactly one student. A tree is a connected undirected graph with $n$ vertices and $n-1$ edges.
Tonight, there are three types of students:
- students who want to party and play music (marked with $\texttt{P}$),
- students who wish to sleep and enjoy silence (marked with $\texttt{S}$), and
- students who don't care (marked with $\texttt{C}$).
Initially, all the edges are thin walls which allow music to pass through, so when a partying student puts music on, it will be heard in every room. However, we can place some thick walls on any edges — thick walls don't allow music to pass through them.
The university wants to install some thick walls so that every partying student can play music, and no sleepy student can hear it.
Because the university lost a lot of money in a naming rights lawsuit, they ask you to find the minimum number of thick walls they will need to use.
InputThe first line contains a single integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.
The first line of each test case contains an integer $n$ ($2 \leq n \leq 10^5$) — the number of vertices in the tree.
The second line of each test case contains $n-1$ integers $a_2, \dots , a_n$ ($1 \leq a_i < i$) — it means there is an edge between $i$ and $a_i$ in the tree.
The third line of each test case contains a string $s$ of length $n$ consisting of characters $\texttt{P}$, $\texttt{S}$, and $\texttt{C}$, denoting that student $i$ is of type $s_i$.
The sum of $n$ over all test cases does not exceed $10^5$.
OutputFor each test case, output a single integer — the minimum number of thick walls needed.
ExampleInput3 3 1 1 CSP 4 1 2 2 PCSS 4 1 2 2 PPSSOutput
1 1 2Note
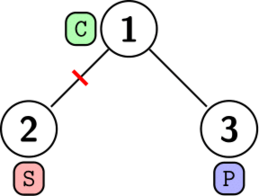
In the first case, we can install one thick wall between rooms $1$ and $2$, as shown below. We cannot install $0$ walls, since then the music from room 3 will reach room 2 where a student wants to sleep, so the answer is $1$. There are other valid solutions.
Output
Vlad有一个儿子非常想去MIT(摩尔达维亚理工学院)。MIT的宿舍可以表示为一个有n个顶点的树形结构,每个顶点代表一个房间,每个房间恰好有一个学生。树是一个有n个顶点和n-1条边的连通无向图。
今晚,学生分为三种类型:
- 想要聚会并播放音乐的学生(用`P`标记),
- 希望安静睡觉的学生(用`S`标记),
- 不关心的学生(用`C`标记)。
最初,所有边都是薄墙,允许音乐通过,所以当一个聚会学生播放音乐时,它会被每个房间听到。然而,我们可以在任何边放置厚墙——厚墙不允许音乐通过。
大学想要安装一些厚墙,使得每个聚会学生都可以播放音乐,同时没有一个睡觉的学生能够听到。
由于大学在一场商标权诉讼中损失了很多钱,他们要求你找出他们需要使用的最少厚墙数量。
**输入数据格式:**
第一行包含一个整数`t`(`1 ≤ t ≤ 1000`)——测试用例的数量。
每个测试用例的第一行包含一个整数`n`(`2 ≤ n ≤ 10^5`)——树中的顶点数。
每个测试用例的第二行包含`n-1`个整数`a_2, …, a_n`(`1 ≤ a_i < i`)——这意味着在树中存在一条边连接`i`和`a_i`。
每个测试用例的第三行包含一个长度为`n`的字符串`s`,由字符`P`、`S`和`C`组成,表示学生`i`的类型是`s_i`。
所有测试用例的`n`之和不超过`10^5`。
**输出数据格式:**
对于每个测试用例,输出一个整数——需要的最少厚墙数量。**题目大意:** Vlad有一个儿子非常想去MIT(摩尔达维亚理工学院)。MIT的宿舍可以表示为一个有n个顶点的树形结构,每个顶点代表一个房间,每个房间恰好有一个学生。树是一个有n个顶点和n-1条边的连通无向图。 今晚,学生分为三种类型: - 想要聚会并播放音乐的学生(用`P`标记), - 希望安静睡觉的学生(用`S`标记), - 不关心的学生(用`C`标记)。 最初,所有边都是薄墙,允许音乐通过,所以当一个聚会学生播放音乐时,它会被每个房间听到。然而,我们可以在任何边放置厚墙——厚墙不允许音乐通过。 大学想要安装一些厚墙,使得每个聚会学生都可以播放音乐,同时没有一个睡觉的学生能够听到。 由于大学在一场商标权诉讼中损失了很多钱,他们要求你找出他们需要使用的最少厚墙数量。 **输入数据格式:** 第一行包含一个整数`t`(`1 ≤ t ≤ 1000`)——测试用例的数量。 每个测试用例的第一行包含一个整数`n`(`2 ≤ n ≤ 10^5`)——树中的顶点数。 每个测试用例的第二行包含`n-1`个整数`a_2, …, a_n`(`1 ≤ a_i < i`)——这意味着在树中存在一条边连接`i`和`a_i`。 每个测试用例的第三行包含一个长度为`n`的字符串`s`,由字符`P`、`S`和`C`组成,表示学生`i`的类型是`s_i`。 所有测试用例的`n`之和不超过`10^5`。 **输出数据格式:** 对于每个测试用例,输出一个整数——需要的最少厚墙数量。