311016: CF1921E. Eat the Chip

E. Eat the Chiptime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Alice and Bob are playing a game on a checkered board. The board has $h$ rows, numbered from top to bottom, and $w$ columns, numbered from left to right. Both players have a chip each. Initially, Alice's chip is located at the cell with coordinates $(x_a, y_a)$ (row $x_a$, column $y_a$), and Bob's chip is located at $(x_b, y_b)$. It is guaranteed that the initial positions of the chips do not coincide. Players take turns making moves, with Alice starting.

On her turn, Alice can move her chip one cell down or one cell down-right or down-left (diagonally). Bob, on the other hand, moves his chip one cell up, up-right, or up-left. It is not allowed to make moves that go beyond the board boundaries.

More formally, if at the beginning of Alice's turn she is in the cell with coordinates $(x_a, y_a)$, then she can move her chip to one of the cells $(x_a + 1, y_a)$, $(x_a + 1, y_a - 1)$, or $(x_a + 1, y_a + 1)$. Bob, on his turn, from the cell $(x_b, y_b)$ can move to $(x_b - 1, y_b)$, $(x_b - 1, y_b - 1)$, or $(x_b - 1, y_b + 1)$. The new chip coordinates $(x', y')$ must satisfy the conditions $1 \le x' \le h$ and $1 \le y' \le w$.

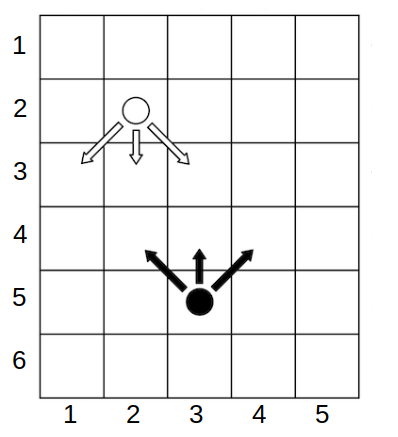Example game state. Alice plays with the white chip, Bob with the black one. Arrows indicate possible moves.

A player immediately wins if they place their chip in a cell occupied by the other player's chip. If either player cannot make a move (Alice—if she is in the last row, i.e. $x_a = h$, Bob—if he is in the first row, i.e. $x_b = 1$), the game immediately ends in a draw.

What will be the outcome of the game if both opponents play optimally?

Input

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of test cases. This is followed by the description of the test cases.

Each test case consists of a single line containing six integers $h$, $w$, $x_a$, $y_a$, $x_b$, $y_b$ ($1 \le x_a, x_b \le h \le 10^6$, $1 \le y_a, y_b \le w \le 10^9$) — the dimensions of the board and the initial positions of Alice's and Bob's chips. It is guaranteed that either $x_a \ne x_b$ or $y_a \ne y_b$.

It is guaranteed that the sum of $h$ over all test cases does not exceed $10^6$.

Output

For each test case, output "Alice" if Alice wins, "Bob" if Bob wins, and "Draw" if neither player can secure a victory. You can output each letter in any case (lowercase or uppercase). For example, the strings "bOb", "bob", "Bob", and "BOB" will be accepted as Bob's victory.

ExampleInput

12
6 5 2 2 5 3
4 1 2 1 4 1
1 4 1 3 1 1
5 5 1 4 5 2
4 4 1 1 4 4
10 10 1 6 10 8
10 10 2 6 10 7
10 10 9 1 8 1
10 10 8 1 10 2
10 10 1 1 2 1
10 10 1 3 4 1
10 10 3 1 1 1

Output

Alice
Bob
Draw
Draw
Draw
Alice
Draw
Draw
Bob
Alice
Alice
Draw

题目大意：
Alice和Bob在一个棋盘上玩游戏。棋盘有h行w列，Alice和Bob各自有一个棋子，初始时分别位于(x_a, y_a)和(x_b, y_b)。两人轮流移动棋子，Alice先手。Alice可以向下、右下或左下移动，Bob可以向上、右上或左上移动。如果移动后的位置超出棋盘边界则不允许移动。如果某玩家将棋子移动到对方棋子所在位置，则该玩家获胜。如果Alice在最后一行或Bob在第一行且无法移动，则游戏以平局结束。输入输出数据格式：每个测试包含多个测试用例。第一行包含一个整数t(1≤t≤10^4)——测试用例的数量。接下来是每个测试用例的描述。每个测试用例包含一行，包含六个整数h, w, x_a, y_a, x_b, y_b(1≤x_a, x_b≤h≤10^6, 1≤y_a, y_b≤w≤10^9)——棋盘的大小和Alice和Bob棋子的初始位置。保证x_a≠x_b或y_a≠y_b。对于每个测试用例，输出“Alice”如果Alice获胜，“Bob”如果Bob获胜，以及“Draw”如果双方都无法获胜。题目大意： Alice和Bob在一个棋盘上玩游戏。棋盘有h行w列，Alice和Bob各自有一个棋子，初始时分别位于(x_a, y_a)和(x_b, y_b)。两人轮流移动棋子，Alice先手。Alice可以向下、右下或左下移动，Bob可以向上、右上或左上移动。如果移动后的位置超出棋盘边界则不允许移动。如果某玩家将棋子移动到对方棋子所在位置，则该玩家获胜。如果Alice在最后一行或Bob在第一行且无法移动，则游戏以平局结束。输入输出数据格式：每个测试包含多个测试用例。第一行包含一个整数t(1≤t≤10^4)——测试用例的数量。接下来是每个测试用例的描述。每个测试用例包含一行，包含六个整数h, w, x_a, y_a, x_b, y_b(1≤x_a, x_b≤h≤10^6, 1≤y_a, y_b≤w≤10^9)——棋盘的大小和Alice和Bob棋子的初始位置。保证x_a≠x_b或y_a≠y_b。对于每个测试用例，输出“Alice”如果Alice获胜，“Bob”如果Bob获胜，以及“Draw”如果双方都无法获胜。