310994: CF1918F. Caterpillar on a Tree

F. Caterpillar on a Treetime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

The caterpillar decided to visit every node of the tree. Initially, it is sitting at the root.

The tree is represented as a rooted tree with the root at the node $1$. Each crawl to a neighboring node takes $1$ minute for the caterpillar.

And there is a trampoline under the tree. If the caterpillar detaches from the tree and falls onto the trampoline, it will end up at the root of the tree in $0$ seconds. But the trampoline is old and can withstand no more than $k$ caterpillar's falls.

What is the minimum time the caterpillar can take to visit all the nodes of the tree?

More formally, we need to find the minimum time required to visit all the nodes of the tree, if the caterpillar starts at the root (node $1$) and moves using two methods.

1. Crawl along an edge to one of the neighboring nodes: takes $1$ minute.
2. Teleport to the root: takes no time, no new nodes become visited.

The second method (teleportation) can be used at most $k$ times. The caterpillar can finish the journey at any node.

Input

The first line of the input contains two integers: $n$ ($2 \le n \le 2\cdot 10^5$) — the number of nodes in the tree, and $k$ ($0 \le k \le 10^9$) — the maximum number of teleports to the root.

The second line contains $n-1$ integers $p_2$, $p_3$, ..., $p_n$ ($1 \le p_i \le n$) — the ancestors in the tree for nodes $2, 3, \ldots, n$; node $1$ is the root.

Output

Print a single number in a single line — the minimum number of minutes required to visit all the nodes of the tree.

ExamplesInput

8 1
1 1 2 2 4 3 3

Output

9

Input

4 0
4 4 1

Output

4

Note

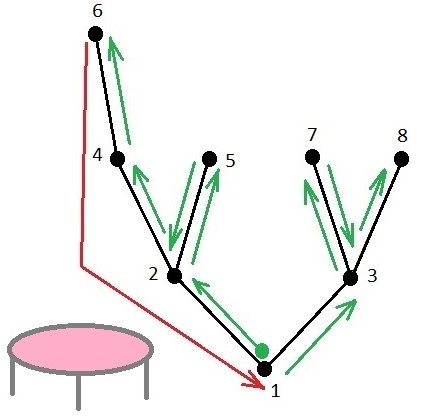
The figure shows one of the ways to traverse the tree from the first test in 9 minutes.

题目大意：
毛毛虫决定访问树上的每个节点。最初，它坐在根节点上。树以根节点为1的有根树表示。每次爬到相邻节点需要1分钟。在树下有一个蹦床。如果毛毛虫从树上脱落并落在蹦床上，它将在0秒内到达树的根。但是蹦床很旧，最多只能承受k次毛毛虫的跌落。求毛毛虫访问树上所有节点的最小时间。

更正式地说，需要找到毛毛虫从根（节点1）开始，使用两种方法移动访问树上所有节点的最小时间。

1. 沿着一条边爬到相邻节点之一：需要1分钟。
2. 传送到根：不花时间，没有新的节点被访问。

第二种方法（传送）最多可以使用k次。毛毛虫可以在任何节点结束旅程。

输入输出数据格式：
输入：
第一行包含两个整数：n（2≤n≤2×10^5）——树中节点的数量，k（0≤k≤10^9）——最大传送回根的次数。
第二行包含n-1个整数p2，p3，...，pn（1≤pi≤n）——树中节点2，3，…，n的祖先；节点1是根。

输出：
打印一行中的单个数字——访问树上所有节点的最小分钟数。

示例：
输入：
8 1
1 1 2 2 4 3 3
输出：
9

输入：
4 0
4 4 1
输出：
4题目大意： 毛毛虫决定访问树上的每个节点。最初，它坐在根节点上。树以根节点为1的有根树表示。每次爬到相邻节点需要1分钟。在树下有一个蹦床。如果毛毛虫从树上脱落并落在蹦床上，它将在0秒内到达树的根。但是蹦床很旧，最多只能承受k次毛毛虫的跌落。求毛毛虫访问树上所有节点的最小时间。 更正式地说，需要找到毛毛虫从根（节点1）开始，使用两种方法移动访问树上所有节点的最小时间。 1. 沿着一条边爬到相邻节点之一：需要1分钟。 2. 传送到根：不花时间，没有新的节点被访问。 第二种方法（传送）最多可以使用k次。毛毛虫可以在任何节点结束旅程。 输入输出数据格式： 输入： 第一行包含两个整数：n（2≤n≤2×10^5）——树中节点的数量，k（0≤k≤10^9）——最大传送回根的次数。 第二行包含n-1个整数p2，p3，...，pn（1≤pi≤n）——树中节点2，3，…，n的祖先；节点1是根。 输出： 打印一行中的单个数字——访问树上所有节点的最小分钟数。 示例： 输入： 8 1 1 1 2 2 4 3 3 输出： 9 输入： 4 0 4 4 1 输出： 4