310900: CF1906I. Contingency Plan 2

I. Contingency Plan 2time limit per test1 secondmemory limit per test1024 megabytesinputstandard inputoutputstandard output

You are working as a manager in The ICPC Company. In the company building, there are $N$ computers (numbered from $1$ to $N$). There are $N - 1$ cables, numbered from $1$ to $N - 1$, that connect all the computers into a single network. Cable $i$ connects computer $U_i$ and $V_i$. Each cable can be set into emergency mode, where cable $i$ only transfers data from computer $U_i$ to computer $V_i$, but not the other way around. During a disaster, it is mandatory for all cables to be in emergency mode.

Through your research, you discover a new way to determine the vulnerability of a network. You want to add zero or more new cables to the current network such that it is not vulnerable during a disaster. Your network is not vulnerable if and only if there is exactly one permutation of $1$ to $N$ such that $u$ appears before $v$ in the permutation for all cables that connect computer $u$ and $v$. In other words, it should have exactly one topological order.

The following illustration shows examples of not vulnerable networks and vulnerable networks.

For the not vulnerable networks, the only permutation that satisfies the requirement for the networks on the left and on the right are $[1, 2, 3]$ and $[3, 1, 2]$, respectively. Meanwhile, for the vulnerable networks, there are $2$ permutations that satisfy the requirement for the network on the left: $[1, 2, 3]$ and $[3, 1, 2]$; while there is no permutation that satisfies the requirement for the network on the right.

You are interested in the minimum number of new cables that should be added to the current network such that it is not vulnerable during a disaster. Furthermore, you want to know, which pairs of computers should be connected by using the minimum number of cables. If there are several ways to connect, you can connect in any way of your choice. Under the given constraints, it can be proven that there exists a way to make the network not vulnerable.

Input

The first line consists of an integer $N$ ($2 \leq N \leq 100\,000$).

Each of the next $N - 1$ lines consists of two integers $U_i$ $V_i$ ($1 \leq U_i, V_i \leq N$). The input edges form a tree.

Output

The first line consists of an integer, representing the minimum number of new cables that should be added to the current network such that it is no longer vulnerable during a disaster. Denote this number as $K$ and the new cables are numbered from $1$ to $K$.

If $K$ is not $0$, then output $K$ lines. Each of the next $K$ lines consists of two integers $A_i$ $B_i$, representing the computers that are connected by the new cable $i$. During a disaster, new cable $i$ only transfers data from computer $A_i$ to computer $B_i$, but not the other way around. If there exist several solutions, you can output any of them.

ExamplesInput

3
1 2
3 2

Output

1
3 1

Input

3
1 2
2 3

Output

0

Input

5
1 2
1 3
3 4
3 5

Output

2
2 3
4 5

Note

Explanation for the sample input/output #3

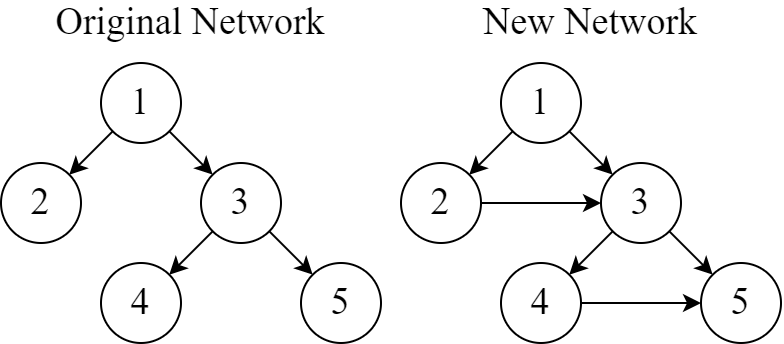
The following illustration shows the original network and the new network with the added cables during a disaster. The only permutation that satisfies the requirement is $[1, 2, 3, 4, 5]$.

题目大意：

你是一家名为 ICPC 公司的经理。公司大楼里有 N 台计算机（编号从 1 到 N）。有 N-1 根电缆（编号从 1 到 N-1），将所有计算机连接成一个单一的网络。电缆 i 连接计算机 U_i 和 V_i。每根电缆可以被设置为紧急模式，其中电缆 i 只从计算机 U_i 向计算机 V_i 传输数据，但不是相反的方向。在灾难期间，所有电缆必须处于紧急模式。

通过你的研究，你发现了一种确定网络脆弱性的新方法。你想在当前网络中添加零或多根新电缆，使得在灾难期间它不是脆弱的。你的网络不是脆弱的，当且仅当有且只有一个从 1 到 N 的排列，使得对于连接计算机 u 和 v 的所有电缆，u 在排列中出现在 v 之前。换句话说，它应该恰好有一个拓扑顺序。

题目要求：

输入数据格式：
- 第一行包含一个整数 N（2 ≤ N ≤ 100,000）。
- 接下来的 N-1 行，每行包含两个整数 U_i 和 V_i（1 ≤ U_i, V_i ≤ N）。输入的边形成一个树。

输出数据格式：
- 第一行包含一个整数，表示应添加到当前网络中的新电缆的最小数量，以使它在灾难期间不再脆弱。设这个数字为 K，新电缆的编号从 1 到 K。
- 如果 K 不是 0，那么输出 K 行。接下来的 K 行，每行包含两个整数 A_i 和 B_i，表示由新电缆 i 连接的计算机。在灾难期间，新电缆 i 只从计算机 A_i 向计算机 B_i 传输数据，但不是相反的方向。如果存在多个解决方案，你可以输出其中任何一个。

请注意，由于 LaTex 格式的限制，上述描述中的变量和格式应以文本形式理解，而不是数学公式。题目大意： 你是一家名为 ICPC 公司的经理。公司大楼里有 N 台计算机（编号从 1 到 N）。有 N-1 根电缆（编号从 1 到 N-1），将所有计算机连接成一个单一的网络。电缆 i 连接计算机 U_i 和 V_i。每根电缆可以被设置为紧急模式，其中电缆 i 只从计算机 U_i 向计算机 V_i 传输数据，但不是相反的方向。在灾难期间，所有电缆必须处于紧急模式。 通过你的研究，你发现了一种确定网络脆弱性的新方法。你想在当前网络中添加零或多根新电缆，使得在灾难期间它不是脆弱的。你的网络不是脆弱的，当且仅当有且只有一个从 1 到 N 的排列，使得对于连接计算机 u 和 v 的所有电缆，u 在排列中出现在 v 之前。换句话说，它应该恰好有一个拓扑顺序。 题目要求： 输入数据格式： - 第一行包含一个整数 N（2 ≤ N ≤ 100,000）。 - 接下来的 N-1 行，每行包含两个整数 U_i 和 V_i（1 ≤ U_i, V_i ≤ N）。输入的边形成一个树。 输出数据格式： - 第一行包含一个整数，表示应添加到当前网络中的新电缆的最小数量，以使它在灾难期间不再脆弱。设这个数字为 K，新电缆的编号从 1 到 K。 - 如果 K 不是 0，那么输出 K 行。接下来的 K 行，每行包含两个整数 A_i 和 B_i，表示由新电缆 i 连接的计算机。在灾难期间，新电缆 i 只从计算机 A_i 向计算机 B_i 传输数据，但不是相反的方向。如果存在多个解决方案，你可以输出其中任何一个。 请注意，由于 LaTex 格式的限制，上述描述中的变量和格式应以文本形式理解，而不是数学公式。