310895: CF1906D. Spaceship Exploration

D. Spaceship Explorationtime limit per test3 secondsmemory limit per test1024 megabytesinputstandard inputoutputstandard output

In The ICPC Galaxy, there exists a zone filled with asteroids that is unsafe to enter. The map of the galaxy is represented in a 2D Cartesian coordinate system. The zone is in the shape of an $N$-sided convex polygon. Each corner is numbered from $1$ to $N$; corner $i$ is located at $(X_i, Y_i)$. At any moment, you should not be inside this polygon; however, it is safe to touch the side of the polygon.

There are $Q$ scenarios (numbered from $1$ to $Q$). In scenario $j$, you want to go from a starting point at $(A_j, B_j)$ to an ending point at $(C_j, D_j)$. You will be riding on a special spaceship that can only travel in a straight line. First, you set the direction of the spaceship, then the spaceship will start traveling in that direction. During the travel, you are only allowed to change direction at most once. Changing direction means you stop the spaceship, set a new direction, and then start traveling again in the new direction.

For each scenario, determine the minimum distance required to travel without being inside of the zone at any moment, or report if it is impossible to reach the ending point.

Input

The first line consists of an integer $N$ ($3 \leq N \leq 100\,000$).

Each of the next $N$ lines consists of two integers $X_i$ $Y_i$ ($-10^9 \leq X_i, Y_i \leq 10^9$). The points form a convex polygon in counterclockwise order. There are no three points which are collinear.

The following line consists of an integer $Q$ ($1 \leq Q \leq 100\,000$).

Each of the next $Q$ lines consists of four integers $A_j$ $B_j$ $C_j$ $D_j$ ($-10^9 \leq A_j, B_j, C_j, D_j \leq 10^9$). There are no starting points and ending points inside the zone. However, it is possible for the starting point and the ending point to be at the side of the zone.

All the coordinates in the input are integers.

Output

For each scenario, output the answer in a single line.

If it is possible to reach the ending point without being inside the zone at any moment, then output the minimum distance required to travel. Otherwise, output -1.

Your answer is considered correct if its absolute error or relative error does not exceed $10^{-6}$. Namely, if your answer is $a$ and the jury's answer is $b$, then your answer is accepted if $\frac{|a - b|}{\max(1, |b|)} \leq 10^{-6}$.

ExamplesInput

5
0 2
2 0
4 0
4 4
2 4
5
6 1 6 3
2 5 0 0
3 5 3 -1
1 4 5 4
3 4 3 0

Output

2
5.6055512755
8.48528137422
4
-1

Input

4
-10 -9
10 -9
10 9
-10 9
2
0 10 0 -10
-10 -10 -10 -10

Output

200.9975124224
0

Input

8
-20 -10
10 -20
25 -15
35 -5
30 10
15 20
-25 15
-30 5
6
-15 -15 -15 20
-30 -5 30 15
25 20 -5 -20
-5 25 20 -20
-30 10 30 -10
-30 -50 50 0

Output

59.0857761929
103.2455532034
94.7213595500
101.5640991922
164.8528137424
94.3398113206

Note

Explanation for the sample input/output #1

This sample is depicted in the following illustration.

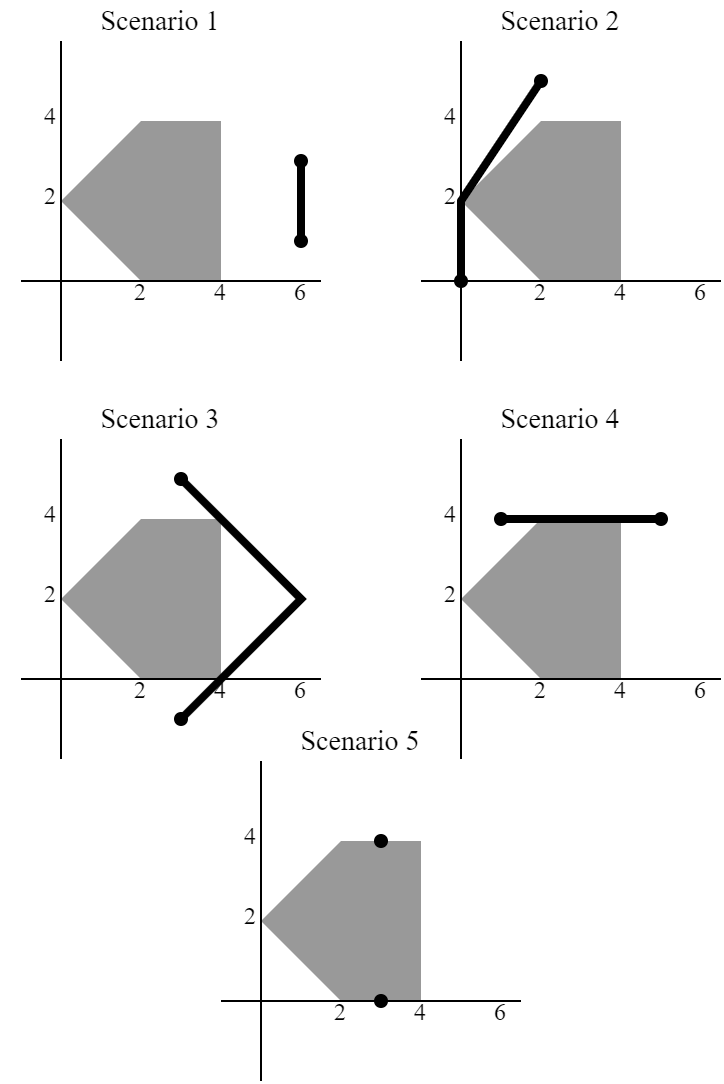
During scenario $1$ and $4$, you can directly go to the ending point without changing the direction.

During scenario $2$, you can go to $(0, 2)$, then change direction to the ending point.

During scenario $3$, you can go to $(6, 2)$, then change direction to the ending point.

During scenario $5$, it can be shown that it is impossible to reach the ending point.

题目大意：在ICPC银河系中，存在一个充满小行星的区域，进入该区域是不安全的。该区域的地图以二维笛卡尔坐标系中的N边形表示。每个顶点从1到N编号；顶点i位于(X_i, Y_i)。在任何时刻，你不应该在这个多边形内部；然而，接触多边形的边是安全的。

有Q个场景（从1到Q编号）。在场景j中，你想从起点(A_j, B_j)去到终点(C_j, D_j)。你将乘坐一艘只能直线行驶的特殊宇宙飞船。首先，你设置宇宙飞船的方向，然后宇宙飞船将开始沿该方向行驶。在行驶过程中，你最多只能改变一次方向。改变方向意味着你停止宇宙飞船，设置一个新的方向，然后再次沿新方向行驶。

对于每个场景，确定在不进入区域内的任何时刻旅行的最小距离，或者报告是否无法到达终点。

输入数据格式：
- 第一行包含一个整数N（3 <= N <= 100,000）。
- 接下来的N行每行包含两个整数X_i Y_i（-10^9 <= X_i, Y_i <= 10^9）。这些点按逆时针顺序形成一个凸多边形。没有三个点是共线的。
- 下一行包含一个整数Q（1 <= Q <= 100,000）。
- 接下来的Q行每行包含四个整数A_j B_j C_j D_j（-10^9 <= A_j, B_j, C_j, D_j <= 10^9）。起点和终点不可能在区域内。然而，起点和终点可能在区域的边上。
- 输入中的所有坐标都是整数。

输出数据格式：
- 对于每个场景，单行输出答案。
- 如果可以在任何时刻不进入区域的情况下到达终点，则输出旅行的最小距离。否则，输出-1。
- 你的答案如果绝对误差或相对误差不超过10^-6，则认为是正确的。即，如果你的答案是a，裁判的答案是b，那么如果|a - b| / max(1, |b|) <= 10^-6，则你的答案是可接受的。题目大意：在ICPC银河系中，存在一个充满小行星的区域，进入该区域是不安全的。该区域的地图以二维笛卡尔坐标系中的N边形表示。每个顶点从1到N编号；顶点i位于(X_i, Y_i)。在任何时刻，你不应该在这个多边形内部；然而，接触多边形的边是安全的。 有Q个场景（从1到Q编号）。在场景j中，你想从起点(A_j, B_j)去到终点(C_j, D_j)。你将乘坐一艘只能直线行驶的特殊宇宙飞船。首先，你设置宇宙飞船的方向，然后宇宙飞船将开始沿该方向行驶。在行驶过程中，你最多只能改变一次方向。改变方向意味着你停止宇宙飞船，设置一个新的方向，然后再次沿新方向行驶。 对于每个场景，确定在不进入区域内的任何时刻旅行的最小距离，或者报告是否无法到达终点。 输入数据格式： - 第一行包含一个整数N（3 <= N <= 100,000）。 - 接下来的N行每行包含两个整数X_i Y_i（-10^9 <= X_i, Y_i <= 10^9）。这些点按逆时针顺序形成一个凸多边形。没有三个点是共线的。 - 下一行包含一个整数Q（1 <= Q <= 100,000）。 - 接下来的Q行每行包含四个整数A_j B_j C_j D_j（-10^9 <= A_j, B_j, C_j, D_j <= 10^9）。起点和终点不可能在区域内。然而，起点和终点可能在区域的边上。 - 输入中的所有坐标都是整数。 输出数据格式： - 对于每个场景，单行输出答案。 - 如果可以在任何时刻不进入区域的情况下到达终点，则输出旅行的最小距离。否则，输出-1。 - 你的答案如果绝对误差或相对误差不超过10^-6，则认为是正确的。即，如果你的答案是a，裁判的答案是b，那么如果|a - b| / max(1, |b|) <= 10^-6，则你的答案是可接受的。