310884: CF1904E. Tree Queries

E. Tree Queriestime limit per test4 secondsmemory limit per test512 megabytesinputstandard inputoutputstandard outputThose who don't work don't eat. Get the things you want with your own power. But believe, the earnest and serious people are the ones who have the last laugh... But even then, I won't give you a present.—Santa, Hayate no Gotoku!

Since Hayate didn't get any Christmas presents from Santa, he is instead left solving a tree query problem.

Hayate has a tree with $n$ nodes.

Hayate now wants you to answer $q$ queries. Each query consists of a node $x$ and $k$ other additional nodes $a_1,a_2,\ldots,a_k$. These $k+1$ nodes are guaranteed to be all distinct.

For each query, you must find the length of the longest simple path starting at node $x^\dagger$ after removing nodes $a_1,a_2,\ldots,a_k$ along with all edges connected to at least one of nodes $a_1,a_2,\ldots,a_k$.

$^\dagger$ A simple path of length $k$ starting at node $x$ is a sequence of distinct nodes $x=u_0,u_1,\ldots,u_k$ such that there exists a edge between nodes $u_{i-1}$ and $u_i$ for all $1 \leq i \leq k$.

Input

The first line contains two integers $n$ and $q$ ($1 \le n, q \le 2 \cdot 10^5$) — the number of nodes of the tree and the number of queries.

The following $n - 1$ lines contain two integers $u$ and $v$ ($1 \le u, v \le n$, $u \ne v$) — denoting an edge between nodes $u$ and $v$. It is guaranteed that the given edges form a tree.

The following $q$ lines describe the queries. Each line contains the integers $x$, $k$ and $a_1,a_2,\ldots,a_k$ ($1 \leq x \leq n$, $0 \leq k < n$, $1 \leq a_i \leq n$) — the starting node, the number of removed nodes and the removed nodes.

It is guaranteed that for each query, $x,a_1,a_2,\ldots,a_k$ are all distinct.

It is guaranteed that the sum of $k$ over all queries will not exceed $2 \cdot 10^5$.

Output

For each query, output a single integer denoting the answer for that query.

ExamplesInput

7 7
1 2
1 3
3 4
2 5
2 6
6 7
2 0
2 1 1
2 2 1 6
3 1 4
3 1 1
5 0
5 2 1 6

Output

3
2
1
4
1
4
1

Input

4 4
1 2
1 3
2 4
2 1 3
3 1 4
2 1 4
2 3 1 3 4

Output

1
2
2
0

Note

In the first example, the tree is as follows:

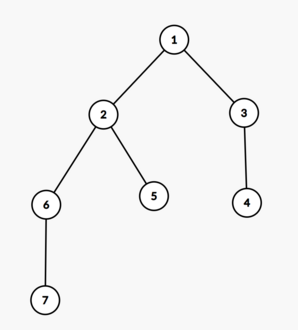
In the first query, no nodes are missing. The longest simple path starting from node $2$ is $2 \to 1 \to 3 \to 4$. Thus, the answer is $3$.

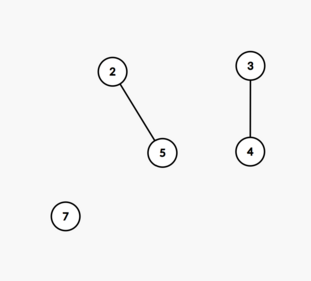
In the third query, nodes $1$ and $6$ are missing and the tree is shown below. The longest simple path starting from node $2$ is $2 \to 5$. Thus, the answer is $1$.

题目大意：
Hayate有一棵有n个节点的树。他想要你回答q个查询。每个查询包含一个节点x和k个其他额外节点a_1, a_2, ..., a_k。这k+1个节点保证都是不同的。对于每个查询，你必须找到在移除节点a_1, a_2, ..., a_k以及所有至少连接到一个节点a_1, a_2, ..., a_k的边之后，从节点x^†开始的最长简单路径的长度。† 一个从节点x开始的长度为k的简单路径是一个不同的节点序列x=u_0, u_1, ..., u_k，使得对于所有1≤i≤k，节点u_{i-1}和u_i之间存在一条边。

输入输出数据格式：
输入：
第一行包含两个整数n和q（1≤n, q≤2*10^5）——树的节点数和查询数。
接下来的n-1行包含两个整数u和v（1≤u, v≤n，u≠v）——表示节点u和v之间的边。保证给定的边构成一棵树。
接下来的q行描述查询。每行包含整数x，k和a_1, a_2, ..., a_k（1≤x≤n，0≤k 保证对于每个查询，x, a_1, a_2, ..., a_k都是不同的。
保证所有查询的k之和不超过2*10^5。

输出：
对于每个查询，输出一个整数，表示该查询的答案。题目大意： Hayate有一棵有n个节点的树。他想要你回答q个查询。每个查询包含一个节点x和k个其他额外节点a_1, a_2, ..., a_k。这k+1个节点保证都是不同的。对于每个查询，你必须找到在移除节点a_1, a_2, ..., a_k以及所有至少连接到一个节点a_1, a_2, ..., a_k的边之后，从节点x^†开始的最长简单路径的长度。† 一个从节点x开始的长度为k的简单路径是一个不同的节点序列x=u_0, u_1, ..., u_k，使得对于所有1≤i≤k，节点u_{i-1}和u_i之间存在一条边。 输入输出数据格式： 输入： 第一行包含两个整数n和q（1≤n, q≤2*10^5）——树的节点数和查询数。 接下来的n-1行包含两个整数u和v（1≤u, v≤n，u≠v）——表示节点u和v之间的边。保证给定的边构成一棵树。 接下来的q行描述查询。每行包含整数x，k和a_1, a_2, ..., a_k（1≤x≤n，0≤k