310865: CF1901F. Landscaping
Description
You are appointed to a very important task: you are in charge of flattening one specific road.
The road can be represented as a polygonal line starting at $(0, 0)$, ending at $(n - 1, 0)$ and consisting of $n$ vertices (including starting and ending points). The coordinates of the $i$-th vertex of the polyline are $(i, a_i)$.
"Flattening" road is equivalent to choosing some line segment from $(0, y_0)$ to $(n - 1, y_1)$ such that all points of the polyline are below the chosen segment (or on the same height). Values $y_0$ and $y_1$ may be real.
You can imagine that the road has some dips and pits, and you start pouring pavement onto it until you make the road flat. Points $0$ and $n - 1$ have infinitely high walls, so pavement doesn't fall out of segment $[0, n - 1]$.
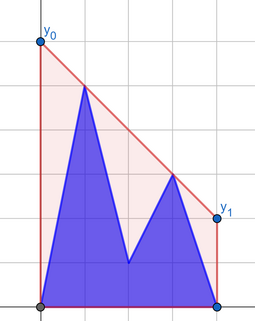
The cost of flattening the road is equal to the area between the chosen segment and the polyline. You want to minimize the cost, that's why the flattened road is not necessary horizontal.
But there is a problem: your data may be too old, so you sent a person to measure new heights. The person goes from $0$ to $n - 1$ and sends you new heights $b_i$ of each vertex $i$ of the polyline.
Since measuring new heights may take a while, and you don't know when you'll be asked, calculate the minimum cost (and corresponding $y_0$ and $y_1$) to flatten the road after each new height $b_i$ you get.
InputThe first line contains a single integer $n$ ($3 \le n \le 2 \cdot 10^5$) — the number of vertices of the polyline.
The second line contains $n$ integers $a_0, a_1, \dots, a_{n - 1}$ ($0 \le a_i \le 10^9$; $a_0 = a_{n - 1} = 0$) — the heights of the corresponding vertices.
The third line contains $n$ integers $b_0, b_1, \dots, b_{n - 1}$ ($0 \le b_i \le 10^9$; $b_0 = b_{n - 1} = 0$) — the new heights of the corresponding vertices.
OutputPrint $n$ numbers: as the $i$-th number ($0$-indexed) print $y_0 + y_1$ of the "best segment" (i. e. the sum of coordinates of the segment that gives the minimum cost) if you already know actual heights $b_0, \dots, b_i$.
If there are several "best segments", print the minimum possible $y_0 + y_1$ among them.
Your answer is considered correct if its absolute or relative error does not exceed $10^{-9}$.
Formally, let your answer be $x$, and the jury's answer be $y$. Your answer is accepted if and only if $\frac{|x - y|}{\max{(1, |y|)}} \le 10^{-9}$.
ExamplesInput5 0 5 1 3 0 0 1 3 2 0Output
8.000000000000 4.000000000000 6.000000000000 6.000000000000 6.000000000000Input
6 0 4 1 3 3 0 0 1 4 0 1 0Output
7.000000000000 5.000000000000 7.500000000000 7.500000000000 6.666666666667 6.666666666667Note
The first answer in the first example is shown on the picture above.
You can achieve the second answer with the following "best segment":
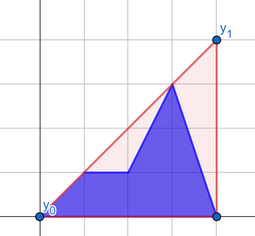
You can achieve the third answer using the following "best segment":
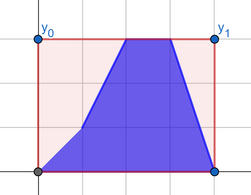
You can achieve the fourth answer with the "best segment" shown below:
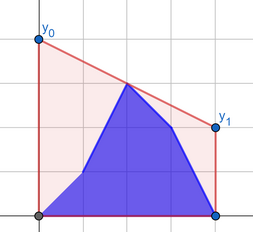
Output
输入数据格式:
- 第一行包含一个整数n(3 ≤ n ≤ 2 * 10^5)——折线的顶点数。
- 第二行包含n个整数a_0, a_1, ..., a_{n - 1}(0 ≤ a_i ≤ 10^9;a_0 = a_{n - 1} = 0)——相应顶点的高度。
- 第三行包含n个整数b_0, b_1, ..., b_{n - 1}(0 ≤ b_i ≤ 10^9;b_0 = b_{n - 1} = 0)——相应顶点的新高度。
输出数据格式:
- 打印n个数:作为第i个数(0索引),如果你已经知道实际高度b_0, ..., b_i,则打印“最佳线段”的y_0 + y_1(即给出最小成本的线段坐标之和)。
- 如果有多个“最佳线段”,则打印它们中y_0 + y_1的最小可能值。
- 你的答案被认为是正确的,如果其绝对误差或相对误差不超过10^-9。
示例输入输出已在题目中给出。题目大意:你被指派了一个非常重要的任务:负责平整一条特定的道路。道路可以表示为一条起点为(0, 0),终点为(n - 1, 0),包含n个顶点(包括起点和终点)的多边形线。这条折线的第i个顶点的坐标是(i, a_i)。平整道路相当于选择从(0, y_0)到(n - 1, y_1)的某个线段,使得折线的所有点都在选定的线段下方(或与线段同高)。y_0和y_1的值可以是实数。你可以想象道路有一些凹陷和坑洞,你开始向其倾倒铺路材料,直到道路变平。点0和n - 1有无限高的墙,所以铺路材料不会从[0, n - 1]段外溢出。平整道路的成本等于选定线段与折线之间的面积。你想要最小化成本,这就是为什么平整后的道路不一定是水平的。但有一个问题:你的数据可能太旧了,所以你派人去测量新的高度。这个人员从0走到n - 1,并给你发送折线每个顶点i的新高度b_i。由于测量新高度可能需要一段时间,而你不知道你何时会被要求,所以在每次获得新的高度b_i后,计算平整道路的最小成本(以及相应的y_0和y_1)。 输入数据格式: - 第一行包含一个整数n(3 ≤ n ≤ 2 * 10^5)——折线的顶点数。 - 第二行包含n个整数a_0, a_1, ..., a_{n - 1}(0 ≤ a_i ≤ 10^9;a_0 = a_{n - 1} = 0)——相应顶点的高度。 - 第三行包含n个整数b_0, b_1, ..., b_{n - 1}(0 ≤ b_i ≤ 10^9;b_0 = b_{n - 1} = 0)——相应顶点的新高度。 输出数据格式: - 打印n个数:作为第i个数(0索引),如果你已经知道实际高度b_0, ..., b_i,则打印“最佳线段”的y_0 + y_1(即给出最小成本的线段坐标之和)。 - 如果有多个“最佳线段”,则打印它们中y_0 + y_1的最小可能值。 - 你的答案被认为是正确的,如果其绝对误差或相对误差不超过10^-9。 示例输入输出已在题目中给出。