310854: CF1900A. Cover in Water
Description
Filip has a row of cells, some of which are blocked, and some are empty. He wants all empty cells to have water in them. He has two actions at his disposal:
- $1$ — place water in an empty cell.
- $2$ — remove water from a cell and place it in any other empty cell.
If at some moment cell $i$ ($2 \le i \le n-1$) is empty and both cells $i-1$ and $i+1$ contains water, then it becomes filled with water.
Find the minimum number of times he needs to perform action $1$ in order to fill all empty cells with water.
Note that you don't need to minimize the use of action $2$. Note that blocked cells neither contain water nor can Filip place water in them.
InputEach test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 100$). The description of the test cases follows.
The first line of each test case contains a single integer $n$ ($1 \le n \le 100$) — the number of cells.
The next line contains a string $s$ of length $n$. The $i$-th character of $s$ is '.' if the cell $i$ is empty and '#' if cell $i$ is blocked.
OutputFor each test case, output a single number — the minimal amount of actions $1$ needed to fill all empty cells with water.
ExampleInput5 3 ... 7 ##....# 7 ..#.#.. 4 #### 10 #...#..#.#Output
2 2 5 0 2Note
Test Case 1
In the first test case, Filip can put water in cells $1$ and $3$. As cell $2$ is between $2$ cells with water, it gets filled with water too.
Test Case 2
In the second case, he can put water sources in cells $3$ and $5$. That results in cell $4$ getting filled with water. Then he will remove water from cell $5$ and place it into cell $6$. As cell $5$'s neighbors, cell $4$ and cell $6$, have water in them, cell $5$ also gets filled with water. You can see the illustration of this case below.
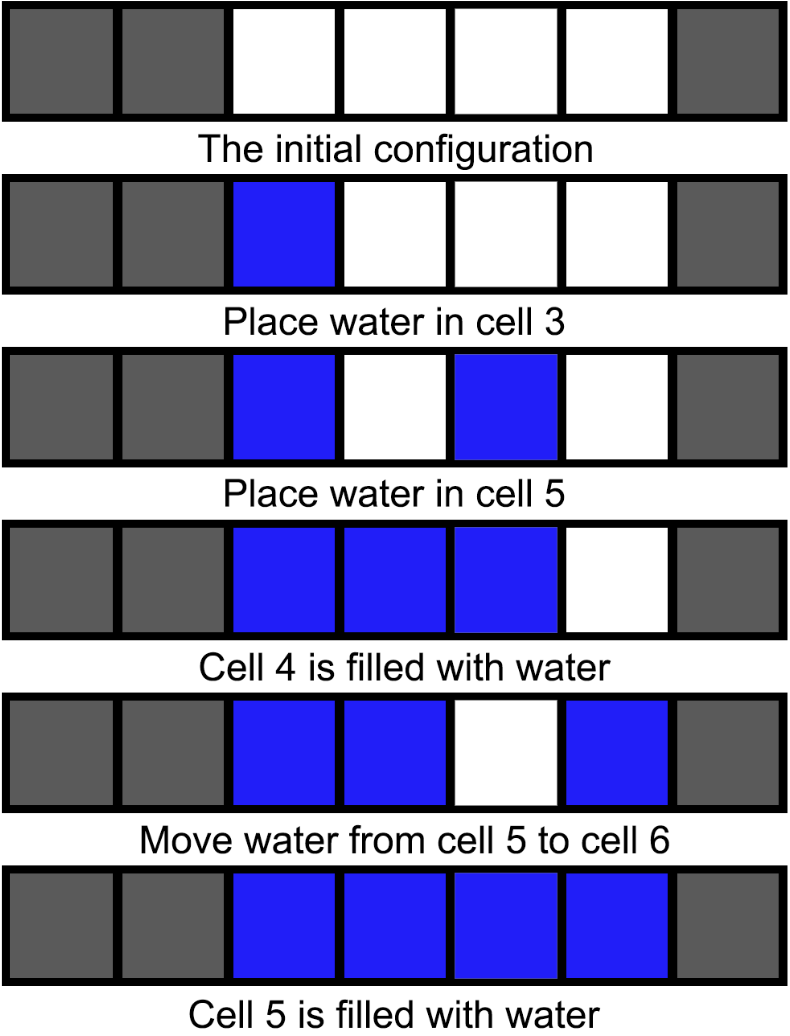 Operations in the second test case. White cells are empty, grey ones are blocked, and blue ones are water.
Operations in the second test case. White cells are empty, grey ones are blocked, and blue ones are water. Test Case 3
In the third case, he can put water in all the empty cells. That requires $5$ actions of type $1$.
Test Case 4
In the fourth case, there are no empty cells. Therefore, he does not have to put any water in them.
Test Case 5
In the fifth test case, there exists a sequence of actions that requires only $2$ type $1$ actions.
Output
Filip有一排单元格,其中一些被阻塞,一些是空的。他希望所有空单元格都有水。他有两种行动方式:
1. 在一个空单元格中放水。
2. 从一个单元格中取水并将其放入任何其他空单元格中。
如果在某个时刻单元格i(2≤i≤n-1)为空,并且单元格i-1和i+1都含有水,那么它就会被水填满。
求他至少需要进行多少次行动1才能使所有空单元格都有水。
输入数据格式:
每个测试包含多个测试用例。第一行包含测试用例的数量t(1≤t≤100)。接下来是每个测试用例的描述。
每个测试用例的第一行包含一个整数n(1≤n≤100)——单元格的数量。
下一行包含一个长度为n的字符串s。如果单元格i为空,则s的第i个字符为'.';如果单元格i被阻塞,则为'#'。
输出数据格式:
对于每个测试用例,输出一个数字——使所有空单元格都有水所需的最小行动1次数。题目大意: Filip有一排单元格,其中一些被阻塞,一些是空的。他希望所有空单元格都有水。他有两种行动方式: 1. 在一个空单元格中放水。 2. 从一个单元格中取水并将其放入任何其他空单元格中。 如果在某个时刻单元格i(2≤i≤n-1)为空,并且单元格i-1和i+1都含有水,那么它就会被水填满。 求他至少需要进行多少次行动1才能使所有空单元格都有水。 输入数据格式: 每个测试包含多个测试用例。第一行包含测试用例的数量t(1≤t≤100)。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数n(1≤n≤100)——单元格的数量。 下一行包含一个长度为n的字符串s。如果单元格i为空,则s的第i个字符为'.';如果单元格i被阻塞,则为'#'。 输出数据格式: 对于每个测试用例,输出一个数字——使所有空单元格都有水所需的最小行动1次数。