310843: CF1898C. Colorful Grid

C. Colorful Gridtime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Elena has a grid formed by $n$ horizontal lines and $m$ vertical lines. The horizontal lines are numbered by integers from $1$ to $n$ from top to bottom. The vertical lines are numbered by integers from $1$ to $m$ from left to right. For each $x$ and $y$ ($1 \leq x \leq n$, $1 \leq y \leq m$), the notation $(x, y)$ denotes the point at the intersection of the $x$-th horizontal line and $y$-th vertical line.

Two points $(x_1,y_1)$ and $(x_2,y_2)$ are adjacent if and only if $|x_1-x_2| + |y_1-y_2| = 1$.

The grid formed by $n=4$ horizontal lines and $m=5$ vertical lines.

Elena calls a sequence of points $p_1, p_2, \ldots, p_g$ of length $g$ a walk if and only if all the following conditions hold:

• The first point $p_1$ in this sequence is $(1, 1)$.
• The last point $p_g$ in this sequence is $(n, m)$.
• For each $1 \le i < g$, the points $p_i$ and $p_{i+1}$ are adjacent.

Note that the walk may contain the same point more than once. In particular, it may contain point $(1, 1)$ or $(n, m)$ multiple times.

There are $n(m-1)+(n-1)m$ segments connecting the adjacent points in Elena's grid. Elena wants to color each of these segments in blue or red color so that there exists a walk $p_1, p_2, \ldots, p_{k+1}$ of length $k+1$ such that

• out of $k$ segments connecting two consecutive points in this walk, no two consecutive segments have the same color (in other words, for each $1 \le i < k$, the color of the segment between points $p_i$ and $p_{i+1}$ differs from the color of the segment between points $p_{i+1}$ and $p_{i+2}$).

Please find any such coloring or report that there is no such coloring.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \leq t \leq 32$). The description of test cases follows.

The only line of each test case contains three integers $n$, $m$, and $k$ ($3 \leq n,m \leq 16$, $1 \leq k \leq 10^9$) — the dimensions of the grid and the number of segments in the walk Elena is looking for.

Output

For each test case, output "NO" if it is not possible to color each of the $n(m-1)+(n-1)m$ segments in blue or red color, so that there exists a walk of length $k+1$ satisfying the condition from the statement.

Otherwise, output in the first line "YES", and then provide the required coloring.

In each of the first $n$ lines of coloring description, output $m-1$ space-separated characters. The $j$-th character in the $i$-th of these $n$ lines should denote the color of the segment between points $(i,j)$ and $(i,j+1)$. Here, use 'B' to denote the blue color and 'R' to denote the red color.

In each of the next $n-1$ lines of coloring description, output $m$ space-separated characters. The $j$-th character in the $i$-th of these $n-1$ lines should denote the color of the segment between points $(i,j)$ and $(i+1,j)$. Similarly, use 'B' to denote the blue color and 'R' to denote the red color.

You can output each letter in the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses, and both 'R' and 'r' are valid notation of red.

ExampleInput

5
4 5 11
3 3 2
3 4 1000000000
3 3 12588
4 4 8

Output

YES
R R B B
R R R R
B B B R
R R B B
R B B R B
R B B B B
B B R R R
NO
NO
YES
R B
B B
B R
B B R
R B B
YES
B B R
R B R
B R R
R R B
B R R B
B B B B
B R R R

Note

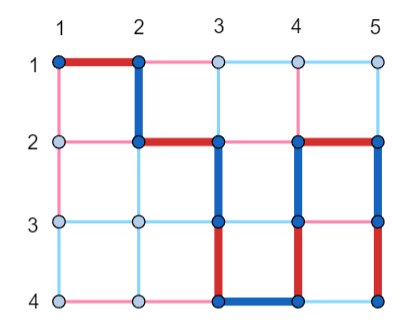
In the first test case, one of the correct answers is shown in the picture below. The color-alternating walk of length $12$ is highlighted.

In the second and the third test cases, it can be shown that there is no coloring satisfying the condition from the statement.

题目大意：
Elena有一个由n条水平线和m条垂直线组成的网格。网格的每个交点由坐标(x, y)表示。两个点相邻当且仅当它们的坐标满足|x1-x2| + |y1-y2| = 1。一个长度为g的点的序列p1, p2, ..., pg称为一个“walk”，当且仅当满足以下条件：序列的第一个点p1是(1, 1)，最后一个点pg是(n, m)，对于每个1 ≤ i < g，pi和pi+1相邻。网格中有n(m-1)+(n-1)m条边。Elena想要将这些边染成蓝色或红色，以便存在一个长度为k+1的walk p1, p2, ..., pk+1，使得这k条边中，没有两条连续的边颜色相同。请找到这样一种染色方案，或者报告不存在这样的染色方案。

输入输出数据格式：
输入：
第一行包含一个整数t，表示测试用例的数量。
接下来每个测试用例包含一行，包含三个整数n, m, k，分别表示网格的尺寸和Elena寻找的walk中边的数量。

输出：
对于每个测试用例，如果不存在满足条件的染色方案，输出"NO"。
否则，首先输出"YES"，然后在接下来的n行中，每行输出m-1个空格分隔的颜色字符（'B'表示蓝色，'R'表示红色），表示第i行从(i,1)到(i,m)的边的颜色。
再在接下来的n-1行中，每行输出m个空格分隔的颜色字符，表示从(1,j)到(n,j)的边的颜色。

示例输入输出：
输入：
5
4 5 11
3 3 2
3 4 1000000000
3 3 12588
4 4 8

输出：
YES
R R B B
R R R R
B B B R
R R B B
R B B R B
R B B B B
B B R R R
NO
NO
YES
R B
B B
B R
B B R
R B B
YES
B B R
R B R
B R R
R R B
B R R B
B B B B
B R R R

注意：在第一个测试案例中，正确的答案之一如下图所示，长度为12的交替颜色的walk被突出显示。在第二个和第三个测试案例中，可以证明不存在满足题目条件的染色方案。题目大意： Elena有一个由n条水平线和m条垂直线组成的网格。网格的每个交点由坐标(x, y)表示。两个点相邻当且仅当它们的坐标满足|x1-x2| + |y1-y2| = 1。一个长度为g的点的序列p1, p2, ..., pg称为一个“walk”，当且仅当满足以下条件：序列的第一个点p1是(1, 1)，最后一个点pg是(n, m)，对于每个1 ≤ i < g，pi和pi+1相邻。网格中有n(m-1)+(n-1)m条边。Elena想要将这些边染成蓝色或红色，以便存在一个长度为k+1的walk p1, p2, ..., pk+1，使得这k条边中，没有两条连续的边颜色相同。请找到这样一种染色方案，或者报告不存在这样的染色方案。 输入输出数据格式： 输入： 第一行包含一个整数t，表示测试用例的数量。 接下来每个测试用例包含一行，包含三个整数n, m, k，分别表示网格的尺寸和Elena寻找的walk中边的数量。 输出： 对于每个测试用例，如果不存在满足条件的染色方案，输出"NO"。 否则，首先输出"YES"，然后在接下来的n行中，每行输出m-1个空格分隔的颜色字符（'B'表示蓝色，'R'表示红色），表示第i行从(i,1)到(i,m)的边的颜色。 再在接下来的n-1行中，每行输出m个空格分隔的颜色字符，表示从(1,j)到(n,j)的边的颜色。 示例输入输出： 输入： 5 4 5 11 3 3 2 3 4 1000000000 3 3 12588 4 4 8 输出： YES R R B B R R R R B B B R R R B B R B B R B R B B B B B B R R R NO NO YES R B B B B R B B R R B B YES B B R R B R B R R R R B B R R B B B B B B R R R 注意：在第一个测试案例中，正确的答案之一如下图所示，长度为12的交替颜色的walk被突出显示。在第二个和第三个测试案例中，可以证明不存在满足题目条件的染色方案。